Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Worksheet on Linear Symmetry
Practice the questions given in the worksheet on linear symmetry.The questions will help us to find whether the given figures possess linear symmetry.
Review the linear symmetry & lines of symmetry and then solve the questions given in the worksheet on linear symmetry in different figures.
1. Write the number of lines of symmetry in the following figures.
(i) Equilateral triangle
(ii) Isosceles triangle
(iii) Scalene triangle
(iv) Square
(v) Rhombus
(vi) Rectangle
(vii) Parallelogram
(viii) Trapezium
(ix) Circle
(x) Semi circle
2. Which letters of English alphabet possess
(i) Vertical line of symmetry
(ii) Horizontal line of symmetry
(iii) Both Horizontal and Vertical line of symmetry
(iv) No line of symmetry
(v) Infinite lines of symmetry
3. Construct the following figures and draw the lines of symmetry in them.
(i) ∆ XYZ such that XY = YZ = ZX = 5 cm
(ii) ∆ ABC such that AB = BC = 3.5 cm and AC = 2 cm
(iii) Square PQRS of side 4 cm
(iv) Rectangle PQRS, PQ = 1.7 cm and QR = 3.8 cm
(v) ∠A = 45°, ∠B = 50° and AB = 3.5 cm
4. Draw the following polygons:
(i) Regular pentagon
(ii) Regular hexagon
(iii) Regular heptagon
(iv) Regular octagon
What can you say about the number of sides and number of lines of symmetry in each?
5. Draw a quadrilateral having the following lines of symmetry.
(i) 0
(ii) 1
(iii) 2
(iv) 4
6. Draw a triangle having the following lines of symmetry.
(i) 0
(ii) 1
(iii) 2
(iv) 3
7. What is other name you can give to the line of symmetry of the following:
(i) Isosceles triangle
(ii) Circle
(iii) Rhombus
(iv) Line segment
(v) Angle
(vi) Equilateral triangle
8. Find the order of rotational symmetry in the following letters:
9. Name any three geometrical figures that possess both lines of symmetry and rotational symmetry
10. Draw two figures that have no line of symmetry but possess rotational symmetry.
11. Draw two figures that possess line of symmetry but no rotational symmetry.
12. Name the figure which neither has line of symmetry nor rotational symmetry.
13. Where does the center of rotation for the following figure lie?
(i) circle
(ii) square
(iii) equilateral triangle
(iv) rectangle
14. Through what angle of rotation are the following figures rotated to find the order of rotation.
(i) Square
(ii) parallelogram
(iii) equilateral triangle
(iv) regular hexagon
(v) circle
15. Find the order of rotational symmetry in the following figures.
(i) Kite
(ii) Rhombus
(iii) Semicircle
(iv) Isosceles trapezium
(v) Isosceles triangle
(vi) Regular hexagon
(vii) Scalene triangle
Answers for the worksheet on linear symmetry are given below to check the exact answers of the above questions on symmetrical lines.
Answers:
1. (i) 3
(ii) 1
(iii) 0
(iv) 4
(v) 2
(vi) 2
(vii) 0
(viii) 4
(ix) infinity
(x) 1
2. (i) A, H, I, M, O, T, U, V, W, X, Y
(ii) B, C, D, E, H, I, K, O, X
(iii) H, I, O, X
(iv) F, G, J, L, N, P, Q, R, S, Z
(v) O
7. (i) bisector of the vertical angle
(ii) diameter
(iii) diagonal
(iv) perpendicular bisector
(v) angular bisector
(vi) median
8. (i) 2
(ii) 2
(iii) infinity
(vi) 2
(v) 2
(vi) 2
(vii) none
9. Rectangle, rhombus, circle
12. Scalene triangle
13. (i) point of intersection of diameters
(ii) point of intersection of diagonals
(iii) centroid
(iv) point of intersection of diagonals
14. (i) 90°
(ii) 180°
(iii) 120°
(iv) 60°
(v) any angle
15. (i) none
(ii) 2
(iii) none
(iv) none
(v) none
(vi) 6
(vii) none
From Worksheet on Linear Symmetry to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
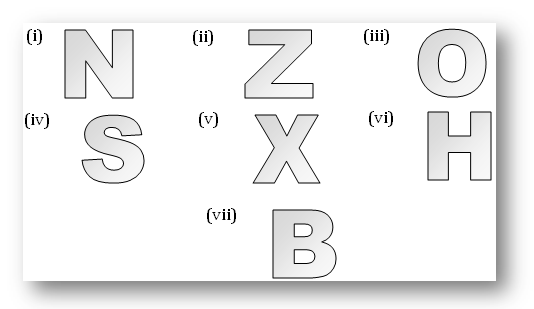


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.