Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Word Problems on L.C.M.
Let us consider some of the word problems on l.c.m. (least common multiple).
1. Find the lowest number which is exactly divisible by 18 and 24.
Solution:
We find the L.C.M. of 18 and 24 to get the required number.
L.C.M. = 2 × 3 × 3 × 4 = 72
Therefore, 72 is the required number.
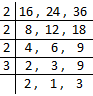
2. Find the lowest number which is less by 5 to be divided by 16, 24 and 36 exactly.
Solution:
We find the L.C.M. of 16, 24 and 36.
L.C.M. = 2 × 2 × 2 × 3 × 2 × 3 = 144
Now subtract 5 from 144 to get the required number.
144 - 5 = 139
Therefore, 139 is the required number.
3. Find the lowest number which is more by 6 to be divided by 25, 40 and 60 exactly.
We find the L.C.M. of 25, 40 and 60.
L.C.M. = 2 × 2 × 5 × 5 × 2 × 3 = 600
Therefore, the required number is 600 + 6 = 606.
4. A shopkeeper sells candles in packets of 12 and candle stands in packet of 8. What is the least number of candles and candle stands Nita should buy so that there will be one candle for each candle stand.
Solution:
To find a quantity which is the lowest common multiple of different quantities, we find the LCM.
Multiples of 12 are 12, 24, 36, 48, ……
Multiples of 8 are 8, 16, 24, 32, 40, ……
The lowest common multiple is 24. So, the least number of candles and candle stand that Nita should buy is 24.
5. Find the lowest number which leaves 3 as remainder when divided by 8, 12 and 16.
Solution:
We find the L.C.M. of 8, 12 and 16.
L.C.M. = 2 × 2 × 2 × 3 × 2 = 48
If we add 3 to 48 it becomes 51 which leaves 3 as remainder when divided by 8, 12 and 16.
Therefore, the required number is 48 + 3 = 51.
6. A florist wants to arrange 24 boquets of flowers in different rows. Find out in how many ways he can arrange the bouquets with same number in each row.
Solution:
We need to find all the factors of 24.
24 = 1 × 24, 24 = 2 × 12, 24 = 3 × 8, 24 = 4 × 6
The factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24
He can arrange rows of 1, 2, 3, 4, 6, 8, 12 and 24 boquets.
From Word Problems on L.C.M. to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 17, 25 12:40 AM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 16, 25 11:46 PM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required… -
Perimeter of a Figure | Perimeter of a Simple Closed Figure | Examples
Jul 16, 25 02:33 AM
Perimeter of a figure is explained here. Perimeter is the total length of the boundary of a closed figure. The perimeter of a simple closed figure is the sum of the measures of line-segments which hav… -
Formation of Numbers | Smallest and Greatest Number| Number Formation
Jul 15, 25 11:46 AM
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,
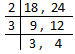
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.