Volume and Surface Area of Cube and Cuboid
Here we will learn how to solve the problems on Volume and Surface Area of Cube and Cuboid:
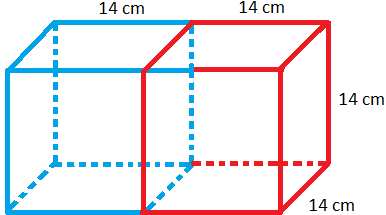
1. Two cubes of edge 14 cm each are joined end to end to form a cuboid. Find the volume and the total surface area of the cuboid.
Solution:
The volume of the cuboid = 2 × volume of one cube
= 2 × 14\(^{3}\) cm\(^{3}\)
= 5488 cm\(^{3}\)
The total surface area of the cuboid = 2(28 × 14 + 14 × 14 + 14 × 28) cm\(^{2}\)
= 2(28 + 14 + 28) × 14 cm\(^{2}\)
= 2(2 × 14 + 1 × 14 + 2 × 14) × 14 cm\(^{2}\)
= 2(2 + 1 + 2) × 14 × 14 cm\(^{2}\)
= 2(5) × 14 × 14 cm\(^{2}\)
= 10× 14 × 14 cm\(^{2}\)
= 1960 cm\(^{2}\)
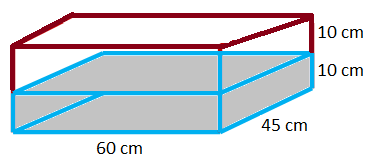
2. The dimensions of the base of a rectangular vessel are 60 cm × 45 cm. Its height is 20 cm. The vessel is half-filled with water. What should be the size of a solid iron cube which when dropped into the vessel will raise the water level up to the brim?
Solution:
The volume of the vessel = 60 × 45 × 20 cm\(^{3}\)
= 54000 cm(^{3}\)
It is half-filled with water
So, the volume of the empty portion of the vessel = \(\frac{1}{2}\) × 54000 cm\(^{3}\)
= 27000 cm\(^{3}\)
The volume of the iron cube should be 27000 cm\(^{3}\) so that it displaces this amount of water and the water level comes up to the brim.
If the edge of the cube is x then,
x\(^{3}\) = 27000 cm\(^{3}\)
⟹ x\(^{3}\) = (30)\(^{3}\) cm\(^{3}\)
⟹ x = 30 cm
Therefore, the edge of the iron cube = 30 cm
The size of the cube should be 30 cm × 30 cm × 30 cm.
From Volume and Surface Area of Cube and Cuboid to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.