Solved Examples on the Basic Properties of Tangents
The solved examples on the basic properties of tangents will help us to understand how to solve different type problems on properties of triangle.
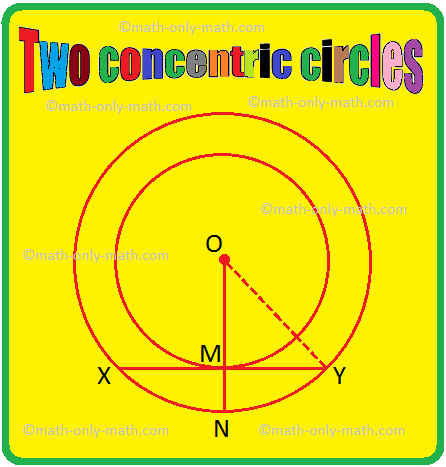
1. Two concentric circles have their centres at O. OM = 4 cm and ON = 5 cm. XY is a chord of the outer circle and a tangent to the inner circle at M. Find the length of XY.
Solution:
Radius OM ⊥ tangent XY. Therefore, OM bisects XY, as ⊥ from centre bisects a chord. So, XY = 2MY. OY = ON = 5 cm. In ∆OMY,
MY^2 = OY^2 – OM^2 = 5^2 cm^2 – 4^2 cm^2 = 25 cm^2 – 16 cm^2 = 9 cm^2.
Therefore, MY = 3 cm. Thus, XY = 6 cm.
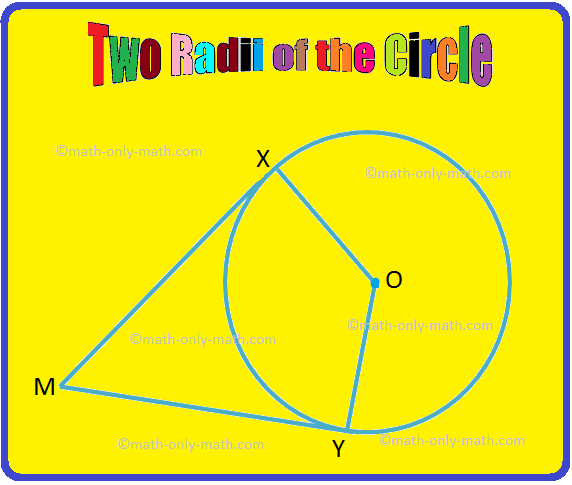
2. In the given figure, OX and OY are two radii of the circle. If MX and MY are tangents to the circle at X and Y respectively, prove that ∠XOY and ∠XMY are supplementary angles.
Solution:
Given: OX and OY are radii and MX and MY are tangents.
To prove: ∠XOY + ∠XMY = 180°.
Proof:
|
Statement |
Reason |
|
1. ∠OXM = 90° |
1. A tangent is perpendicular to the radius drawn through the point of contact. |
|
2. ∠OYM = 90° |
2. As in 1. |
|
3. ∠OXM + ∠XMY + ∠OYM + ∠XOY = 360° ⟹ 90° + ∠XMY + 90° + ∠XOY = 360° ⟹ ∠XMY + ∠XOY = 360° – 180° ⟹ ∠XOY + ∠XMY = 360° – 180° |
3. The sum of the four angles of a quadrilateral is 360°. From statements 1 and 2. |
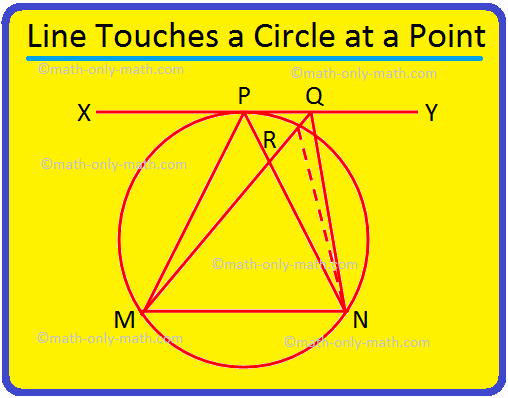
3. If a line XY touches a circle at P and MN is a chord of the circle then prove that ∠MPN > ∠MQN, where Q is any point on XY other than P.
Solution:
Given: MN is a chord of a circle and tyhe tangent at the point P is the line XY. Q is any other point on XY.
To prove: ∠MPN > ∠MQN.
Proof:
|
Statement |
Reason |
|
1. MQ will cut the circle at a point R. Join R to N. |
1. XY is tangent at P and so all points of XY except P are outside the circle. |
|
2. ∠MPN = ∠MRN. |
2. Angles in the same segment are equal. |
|
3. ∠MRN > ∠RQN |
3. Exterior angle is greater than interior opposite angle in a triangle. |
|
4. ∠MPN > ∠RQN = ∠MQN. |
4. By statements 2 and 3. |
From Solved Examples on the Basic Properties of Tangents to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 14, 24 02:12 PM
2nd grade geometry worksheet -
2nd grade math Worksheets | Free Math Worksheets | By Grade and Topic
Dec 14, 24 12:25 PM
2nd grade math worksheets is carefully planned and thoughtfully presented on mathematics for the students. -
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Dec 13, 24 08:43 AM
We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only r… -
Patterns in Math | Missing Number | Counting Numbers | Worksheets
Dec 13, 24 12:31 AM
Finding patterns in math is very important to understand the sequence in the series. We need to find the exact missing number that from the group of numbers. The counting numbers may be counting -
Concept of Pattern | Similar Patterns in Mathematics | Similar Pattern
Dec 12, 24 11:22 PM
Concept of pattern will help us to learn the basic number patterns and table patterns. Animals such as all cows, all lions, all dogs and all other animals have dissimilar features. All mangoes have si…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.