Reduction Transformation

We will discuss here about the similarity on Reduction transformation.

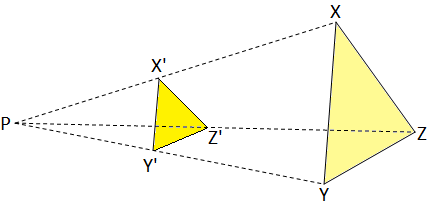
In the figure given below ∆X’Y’Z’ is a reduced image of ∆XYZ. 

The two triangles are similar. Here also the triangles are equiangular and \(\frac{X’Y’}{XY}\) = \(\frac{Y’Z’}{YZ}\) = \(\frac{Z’X’}{ZX}\) = k.

Here k is known as the reduction factor and P is known as the centre of reduction.

Therefore, in a size transformation, a given figure undergoes enlargement or reduction by a scale factor k, such that the resulting figure is similar to the original figure, i.e., the image retains the shape of the original object.

If ∆XYZ is transformed to ∆X’Y’Z’ by a scale factor k about the point P, we get \(\frac{PX’}{PX}\) = \(\frac{PY’}{PY}\) = \(\frac{PZ’}{PZ}\) = k.

2. A rectangle PQRS has been reduced to a rectangle P’ Q’ R’ S’ and their areas are 192 cm\(^{2}\) and 12 cm\(^{2}\) respectively. If Q’ R’ is 3 cm, then find QR.

Solution:

Let \(\frac{area of P’ Q’ R’ S’}{area of PQRS}\) = k\(^{2}\)

Therefore, \(\frac{12 cm\(^{2}\)}{192 cm\(^{2}\)}\) = k\(^{2}\)

⟹ \(\frac{1}{16}\) k\(^{2}\)

⟹ k = \(\frac{1}{4}\)

Now, \(\frac{Q’ R’}{QR}\) = k

⟹ \(\frac{3 cm}{QR}\) = \(\frac{1}{4}\)

⟹ QR = 12 cm

9th Grade Math

From Reduction Transformation to HOME PAGE

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit