Subscribe to our YouTube channel for the latest videos, updates, and tips.


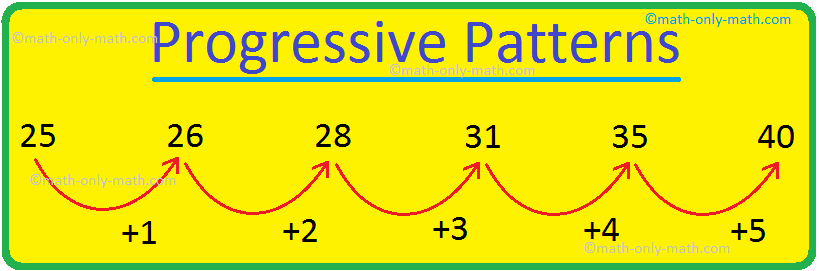
Progressive Patterns

A pattern that increases or decreases in two or more ways are called progressive patterns.

These patterns are combination of more than one change. It can very in combination of size, color and value.

Logmar charts used by opmalmologists for vision test is an example of progressive pattern.

Observe pattern in the following sequence and identify the rule.

Progressive Patterns

Questions and Answers on Progressive Patterns:

1. Find the missing pair in the pattern.

(i) (3, 9), (5, 15), (_____, _____), (9, 27)

(ii) (1, 7), (3, 21), (5, 35), (_____, _____).

(iii) 90, 85, 100, 95, 110, _____, _____.

(iv) 1, 2, 4, 7, 11, 16, _____, _____.

(v) A, AB, ABC, ABCD, _____, _____.

(vi) 180, 130, 90, _____, _____.


Answers:

1. (i) (7, 21)

(ii) (7, 49)

(iii) 105, 120

(iv) 22, 29

(v) ABCDE, ABCDEF

(vi) 60, 40.


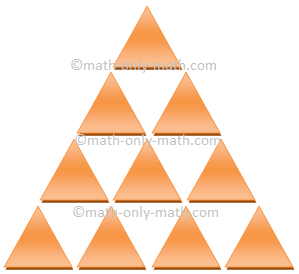
2. Identify the type of pattern in the following figure.

Progressive Patterns Question

Answer:

Progressive pattern




Math Patterns 

Math Homework Sheets 

From Progressive Patterns to HOME PAGE




Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.



New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.




Share this page: What’s this?

Recent Articles

RSS

  1. Worksheet on Average | Word Problem on Average | Questions on Average

    May 17, 25 05:37 PM

    In worksheet on average interest we will solve 10 different types of question. Find the average of first 10 prime numbers. The average height of a family of five is 150 cm. If the heights of 4 family

    Read More

  2. How to Find the Average in Math? | What Does Average Mean? |Definition

    May 17, 25 04:04 PM

    Average 2
    Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities.

    Read More

  3. Problems Based on Average | Word Problems |Calculating Arithmetic Mean

    May 17, 25 03:47 PM

    Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed.

    Read More

  4. Rounding Decimals | How to Round a Decimal? | Rounding off Decimal

    May 16, 25 11:13 AM

    Round off to Nearest One
    Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate

    Read More

  5. Worksheet on Rounding Off Number | Rounding off Number | Nearest 10

    May 15, 25 05:12 PM

    In worksheet on rounding off number we will solve 10 different types of problems. 1. Round off to nearest 10 each of the following numbers: (a) 14 (b) 57 (c) 61 (d) 819 (e) 7729 2. Round off to

    Read More