Problems on Right Circular Cylinder

Here we will learn how to solve different types of problems on right circular cylinder.

1. A solid, metallic, right circular cylindrical block of radius 7 cm and height 8 cm is melted and small cubes of edge 2 cm are made from it. How many such cubes can be made from the block?

Solution:

For the right circular cylinder, we have radius (r) = 7 cm, height (h) = 8 cm.

Therefore, its volume = πr$^{2}$h

                               = $\frac{22}{7}$ × 7$^{2}$ × 8 cm$^{3}$

                               = 1232 cm³

The volume of a cube = (edge)$^{3}$

                                = 2$^{3}$ cm$^{3}$

                                = 8 cm$^{3}$

Therefore, the number of cubes that can be made = volume of the cylinder/volume of a cube

                                                                        = $\frac{1232 cm^{3}}{8cm^{3}}$

                                                                        = 154

Therefore, 154 cubes can be made from the block.

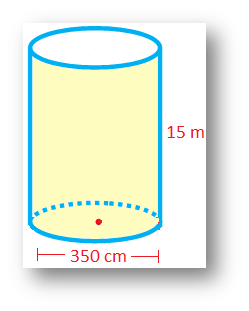
2. The height of a cylindrical pillar is 15 m. The diameter of its base is 350 cm. What will be the cost of painting the curved surface of the pillar at Rs 25 per m$^{2}$?

Solution:

The base is circular and so the pillar is a right circular cylinder.

Here, radius = 175 cm = 1.75 m and height = 15 m

Therefore, the curved surface area of the pillar = 2πrh

                                                                    = 2 × $\frac{22}{7}$ × 1.75 × 15 m$^{2}$

                                                                    = 165 m$^{2}$

Therefore, the cost of painting this area = Rs 25 × 165 = Rs 4125.

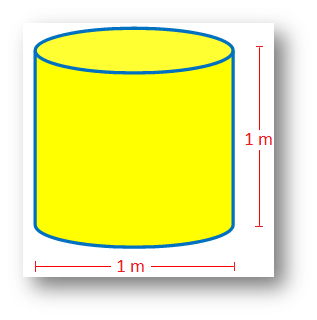
3. A cylindrical container is to be made of tin. The height of the container is 1 m and the diameter of the base is 1 m. If the container is open at the top and tin sheet costs Rs 308 per m$^{2}$, what will be the cost of tin for making the container?

Solution:

Given, diameter of the base is 1 m.

Here, radius = r = $\frac{1}{2}$ m and height = h = 1 m.

Total area of tin sheet required = curved surface area + area of the base

                                              = 2πrh + πr$^{2}$

                                              = πr(2h + r)

                                              = π ∙ $\frac{1}{2}$ ∙ (2 × 1 + $\frac{1}{2}$) m$^{2}$

                                              = $\frac{5π}{4}$ m$^{2}$

                                              = $\frac{5}{4}$ ∙  $\frac{22}{7}$m$^{2}$

                                              = $\frac{55}{14}$ m$^{2}$

Therefore, the cost of tin = Rs 308 × $\frac{55}{14}$ = Rs 1210.

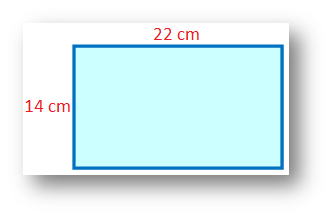
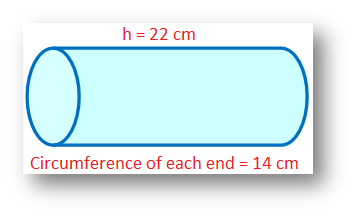
4. The dimensions of a rectangular piece of paper are 22 cm × 14 cm. It is rolled once across the breadth and once across the length to form right circular cylinders of biggest possible surface areas. Find the difference in volumes of the two cylinders that will be formed.

Solution:

When rolled across the breadth

Circumference of the cross section = 14 cm and height = 22 cm

Therefore, 2πr = 14 cm

or, r = $\frac{14}{2π}$ cm

or, r = $\frac{14}{2 × \frac{22}{7}}$ cm

or, r = $\frac{49}{22}$ cm

When rolled across the length

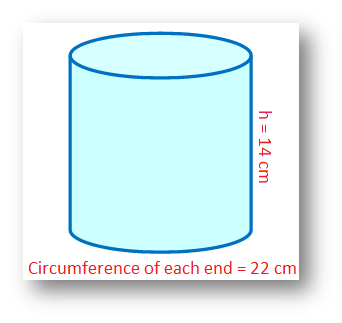
Circumference of the cross section = 22 cm and height = 14 cm

Therefore, 2πR = 22 cm

or, R = $\frac{22}{2π}$ cm

or, r = $\frac{22}{2 × \frac{22}{7}}$ cm

or, r = $\frac{7}{2}$ cm

Therefore, volume = πR$^{2}$h

                           = $\frac{22}{7}$ × ($\frac{7}{2}$)$^{2}$ × 14 cm$^{3}$

                           = 11 × 49 cm$^{3}$

Therefore, the difference in volumes = (11 × 49 - 7 × 49) cm$^{3}$

                                                     = 4 × 49 cm$^{3}$

                                                     = 196 cm$^{3}$

Therefore, 196 cm$^{3}$ is the difference in volumes of the two cylinders.

9th Grade Math

From Problems on Right Circular Cylinder to HOME PAGE