Problems on Common Tangents to Two Circles
Here we will solve different types of problems on common tangents to two circles.
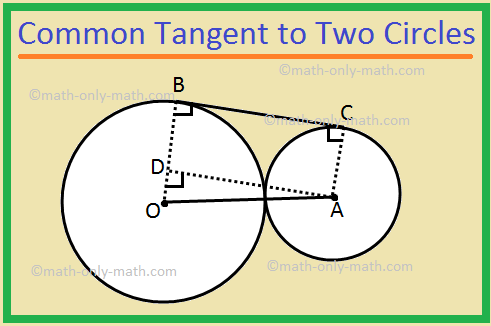
1. There are two circles touch each other externally. Radius of the first circle with centre O is 8 cm. Radius of the second circle with centre A is 4 cm. Find the length of their common tangent BC.
Solution:
Join O to A and B. Join A to C. Draw DA ⊥ OB.
Now DA = BC, as they are opposite sides of rectangle ACBD.
OA = 8 cm + 4 cm
= 12 cm.
OD = 8 cm – 4cm
= 4 cm.
Therefore, DA = \(\sqrt{OA^{2} - OD^{2}}\)
= \(\sqrt{12^{2} - 4^{2}}\) cm
= \(\sqrt{144 - 16}\) cm
= \(\sqrt{128}\) cm
= 8√2 cm
Therefore, BC = 8√2 cm.
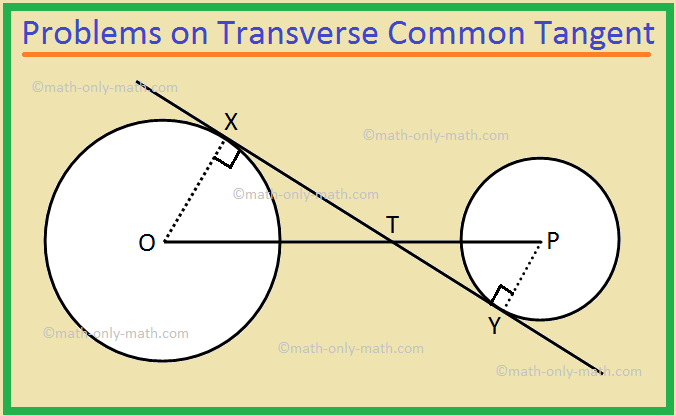
2. Prove that a transverse common tangent drawn to two circles divides the line joining their centres into the ratio of their radii.
Solution:
Given: Two circles with centres O and P, and radii OX and PY respectively. The transverse common tangent XY touches them at X and Y respectively. XY cuts OP at T.
To prove: \(\frac{OT}{TP}\) = \(\frac{OX}{PY}\).
Proof:
|
Statement |
Reason |
|
1. In ∆XOT and ∆YPT, (i) ∠OXT = ∠PYT = 90 ° (ii) ∠OTX = ∠PTY. |
1. (i) Tangent ⊥ Radius. (ii) Vertically opposite angles. |
|
2. ∆XOT ∼ ∆YPT |
2. By A – A criterion of similarity. |
|
3. Therefore, \(\frac{OT}{TP}\) = \(\frac{OX}{PY}\). (Proved) |
3. Corresponding sides of similar triangles are proportional. |
From Problems on Common Tangents to Two Circles to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.