Multiplication and Division of Units of Measurement

We will learn how to multiply and divide of units of measurement.

We carry out multiplication and division of measurements as we do for decimal numbers.

Multiplication of Units of Length:

We can multiply lengths by a number like multiplication of ordinary numbers.

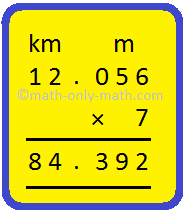
1. Multiply 12 km 56 m by 7.

Solution:                                         

12 km 56 m = 12.056 km

Hence, 12.056 × 7 = 84.392 km

2. Multiply 44 dam 28 cm by 12

Solution:

28 cm = 0.28 m

1 dam = 10 m

28 cm = 0.028 dam

Hence, 44 dam 28 cm × 12 = 528.336

3. Multiply 7 km 346 m by 6

Solution:

We first convert km and m into m and then multiply.

7 km 346 m = 7000 m + 346 m = 7346 m Now we multiply by 6 = 7346 × 6 = 44076 m

To convert 44076 m to km we separate the last 3 digits from the right and write there as m.

44076 m = 44 km 76 m

Hence, 7 km 346 m by 6 =44 km 76 m

4. Multiply 15 m 326 mm by 6

Step I: 326 × 6 = 1956 mm                           = 1000 mm + 956 mm                           = 1 m 956 mm Step II: Write 956 under millimetres and carry 1 to metres. 15 × 6 = 90 90 + 1 = 91 m Step III: Write 91 under metres.

Therefore, 15 m 326 mm × 6 = 91 m 956 mm

Multiplication of Units of Mass:

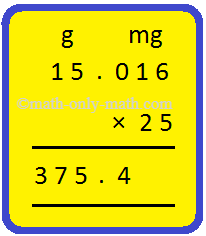
1. Multiply 15 g 16 mg by 25

Solution:

16 mg = $\frac{16}{1000}$ g

15 g 16 mg = 15.016 g

Hence, 15 g 16 mg × 25 = 375.4 g

2. Multiply 7 kg 4 hg 6 dag 7 g by 15.

Step I: Multiply grams. 7 × 15 = 105 g 105 g = 10 dag 5 g Step II: Write 5 under grams and carry 10 to dag. Step III: Multiply decagrams. 6 × 15 = 90 90 + 10 = 100 dag 100 dag = 10 hg 0 dag Step III: Write 0 under dag and carry 10 to hectograms. Step IV: Multiply hectograms    4 × 15 = 60 60 + 10 = 70 hg 70 hg = 7 kg 0 hg Step V: Write 0 under hectogram and carry 7 to kilograms. Step VI: Multiply kilograms. 7 × 15 = 105 kg 105 + 7 = 112 kg

Multiplication of Units of Capacity:

We can multiply the units of capacity measures l and ml by a number like ordinary numbers.

1. Multiply 9 dℓ 72 mℓ by 6

Solution:

72 mℓ = $\frac{72}{100}$ dℓ = 0.72 dℓ

9 dℓ 72 mℓ = 9.72 dℓ

Hence, 9.72 dℓ × 6 = 58.32 dℓ

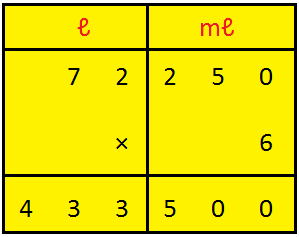
2. Multiply 72 ℓ 250 mℓ by 6

Solution: First convert 72 l 250 ml into ml. 72 l 250 ml = 72 × 1000 ml + 250 ml                      = 72000 ml + 250 ml                      = 72250 ml 72250 × 6 = 433500 ml                    = 433 l 500 ml

Hence, 72 l 250 ml × 6 = 433 l 500 ml

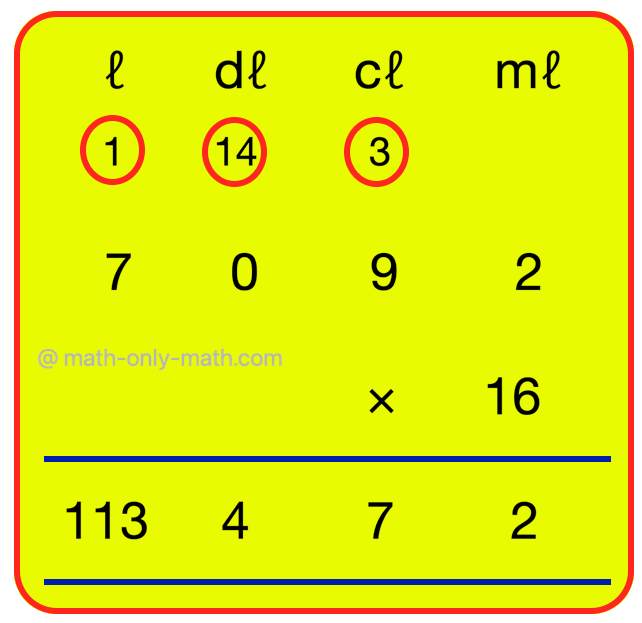
3. Multiply 7 l 9 cl 2 ml by 16

Step I: Write the units in order. Step II: Since decilitre is missing in the question, put 0 in its place. Step III: Multiply millilitres 2 × 16 = 32 ml              3 cl + 2 ml Carry 3 to the centilitres and write 2 under millilitres. Step IV: Multiply centilitres. 9 × 16 = 144 cl + 3 = 147 cl = 14 dl + 7 cl Step V: Write 7 under centilitres and carry 14 to decilitres Step VI: Multiply decilitres 0 × 16 = 0            0 + 14 = 14 dl = 1 l 4 dl Step VII: Write 4 under decilitres and carry 1 to the litres. Step VIII: Multiply litres 7 × 16 = 112 l               112 + 1 = 113 l Step IX: Write 113 under litres Therefore, 7 l 9 cl 2 ml × 16 = 113 l 4 dl 7 cl 2 ml = 113 l 472 ml

Division of Units of Length:

We can divide lengths by a number like division of ordinary numbers. If the measurement is given as a combination of two units like km and m or m and cm, we first convert higher unit to lower unit and then divide.

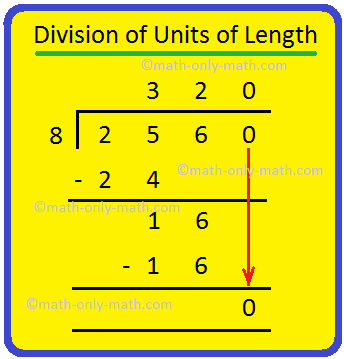
1. Divide 2 km 560 m unit by 8.

Solution:

Let us convert 2 km 560 m into m. 2 km 560 m = 2000 m + 560 m = 2560 m Now, divide 2560 by 8

Hence, 2 km 560 m ÷ 8 = 320 m

Division of Units of Mass:

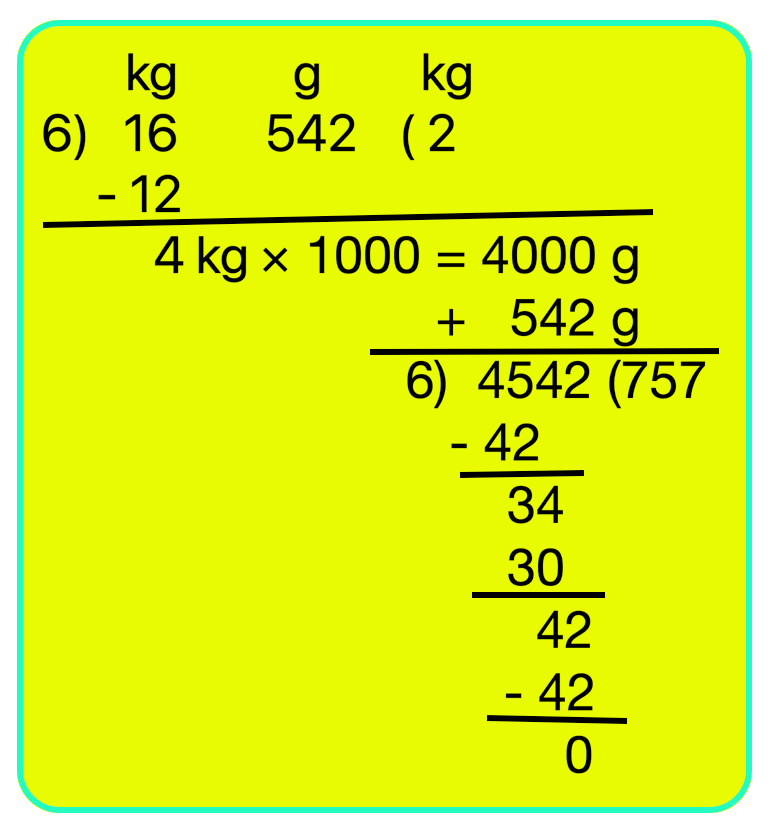
1. Divide 16 kg 542 g by 6

First Method	Second Method
	16 kg 542 g = 16.542 kg

16 kg 542 g ÷ 6 = 2 kg 757 g

                         = 2.757 kg

Division of Units of Capacity:

We can divide units of capacity measures l and ml by a number like ordinary numbers.

1. Divide 132 ℓ 64 dℓ by 8

Solution:

64 dℓ = 6.4 ℓ

132 ℓ 64 dℓ = 138.4 ℓ

Hence, 138.4 ℓ ÷ 8 = 17.3 ℓ

2. Divide 60 l 750 ml by 5

Solution: When measurements are given as combination of two units, we first convert the bigger unit to lower unit and then divide. 60 l 750 ml = 60 l + 750 ml                  = 60000 ml + 750 ml                  = 60750 ml Now divide 60750 by 5 60750 ÷ 5 = 12150 ml                 = 12000 ml + 150 ml                 = 12 l 150 ml

Hence, 60 l 750 ml ÷ 5 = 12 l 150 ml

3. Divide 717 l 32 ml by 8

Solution:

717 l 32 ml = 717000 ml + 32 ml

                  = 717032 ml

Therefore, 717 l 32 ml ÷ 8 = 89629 ml

                                         = 89 l 629 ml

Questions and Answers on Multiplication and Division of Units of Measurement:

1. Multiply the following metric measures of length.

(i) 16 m by 7

(ii) 70 dm 4 cm by 24

(iii) 22 km by 10

(iv) 84 km 560 m by 51

(v) 34 cm by 25

(vi) 48 cm 9 mm by 62

(vii) 26 m 24 cm by 30

(viii) 80 m 5 cm by 10

Answers:

1. (i) 112 m

(ii) 1689 dm 6 cm

(iii) 220 km

(iv) 4312 km 560 m

(v) 850 cm

(vi) 3031 cm 8 mm

(vii) 78 m 720 cm

(viii) 800 m 50 cm

2. Multiply the following:

(i) 8 kg 225 g × 12 

(ii) 12 km 450 m × 17 

(iii) 7 kl 3 hl 4 dal × 6 

(iv) 5 m 4 dm 8 cm 9 mm × 11

(v) 45 m 28 cm × 8 

(vi) 115 kg 25 g × 14

Answer:

2. (i) 98.7 kg

(ii) 211.65 km

(iii) 44.04 kl

(iv) 60.379 m

(v) 362.24 m

(vi) 1610.35 kg

3. Divide the following metric measures of length.

(i) 240 km by 6

(ii) 14 km 580 m by 12

(iii) 36 m by 18

(iv) 50 cm 4 mm by 7

(v) 72 m by 8

(vi) 62 m 8 cm by 4

Answers:

3. (i) 40 km

(ii) 1 km 215 m

(iii) 2 m

(iv) 7 cm 2 mm

(v) 9 m

(vi) 15 m 52 cm

4. Divide the following:

(i) 40 km 320 m ÷ 5

(ii) 85 m 67 cm ÷ 13

(iii) 12 kg 264 g ÷ 12

(iv) 13 l 4 dl 8 cl 2 ml ÷ 9

(v) 116 km 280 m ÷ 12

(vi) 2 kg 800 g ÷ 14

Answer:

4. (i) 8.064 km

(ii) 6.59 m

(iii) 1.022 kg

(iv) 1.498 l

(v) 9.69 km

(vi) 0.2 kg

5. Solve the given:

(i) 56 km × 32

(ii) 32 km 124 m × 4 

(iii) 30 m 75 cm ÷ 15

(iv) 47 cm 6 mm ÷ 20

(v) 66 dm 3 cm × 61

Answers:

5. (i) 1792 km

(ii) 128 km 496 m 

(iii) 2 m 5 cm

(iv) 23 cm 8 mm

(v) 4044 dm 3 cm

6. Multiply the following Metric Measures of Capacity:

(i) 5 l 750 ml × 4

(ii) 12 l 125 ml × 22

(iii) 13 l 124 ml × 10

(iv) 14 l 120 ml × 7

(v) 44 l 85 ml × 15

(vi) 18 l 33 ml × 51

Answers:

6. (i) 23 l

(ii) 266 l 750 ml

(iii) 131 l 240 ml

(iv) 98 l 840 ml

(v) 661 l 275 ml

(vi) 919 l 683 ml

7. Divide the following metric measures of Capacity.

Ron, Sam, Mary and Jack were given different measuring jars. All of them were asked to fill a 1 l Can using their jars. Find out how many times each one of them have to fill their jars and pours them in their Can.

Answers:

7. (i) 2 times

(ii) 5 times

(iii) 10 times

(iv) 20 times

5th Grade Numbers

5th Grade Math Problems

From Multiplication and Division of Units of Measurement to HOME PAGE