H.C.F. of Polynomials by Division Method
Now we will learn how to find the H.C.F. of polynomials by division method. We already learnt how to find out the H.C.F. by factorization of those polynomials which can easily be factorized by the method of factorization of second degree and third degree expressions. But now we will learn that if the number of terms in the given expression is 4 or more than 4 and the power of the variables is 3 or more than 3 and they cannot be easily factorized by the known methods of factorization, then to determine the H.C.F. of those expressions, we need to use the long division method.
1. Find the H.C.F. of 3m3 – 12m2 + 21m – 18 and 6m3 – 30m2 + 60m – 48 by using the division method.
Solution:
(i) The given two expressions are arranged in the descending order of powers of the variable ‘m’.
(ii) Separating the common factors between the terms of the expressions, we get
|
3m3 – 12m2 + 21m – 18 = 3(m3 – 4m2 + 7m – 6) |
6m3 – 30m2 + 60m – 48 = 6(m3 – 5m2 + 10m – 8) |
Therefore, the common factors of the two expressions are 3 and 6. The H.C.F. of 3 and 6 is 3. In the last step 3 is multiplied with the divisor obtained by division method.
Thus, the H.C.F. of m3 – 4m2 + 7m – 6 and m3 – 5m2 + 10m – 8 = (m – 2)
Therefore, the H.C.F. of 3m3 – 12m2 + 21m – 18 and 6m3 – 30m2 + 60m – 48 = 3 × (m – 2) = 3(m – 2)
2. Determine the H.C.F. of a4 + 3a3 + 2a2 + 3a + 1, a3 + 4a2 + 4a + 1 and a3 + 5a2 + 7a + 2 by using the division method.
Solution:
(i) The given three expressions are arranged in the descending order of powers of the variable ‘a’.
(ii) We see that there are no common factors between the terms of the given three expressions.
So, by using the method of long division we get,
So, we observe that a2 + 3a + 1 is the H.C.F. of the first two expressions. Now let us see whether a2 + 3a + 1 is a factor of third expression or not. Again, we observe that third expression ‘a3 + 5a2 + 7a + 2’ is exactly divisible by a2 + 3a + 1.
Therefore, the H.C.F. of a4 + 3a3 + 2a2 + 3a + 1, a3 + 4a2 + 4a + 1 and a3 + 5a2 + 7a + 2 = a2 + 3a + 1.
8th Grade Math Practice
From H.C.F. of Polynomials by Division Method to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns
Dec 13, 24 08:37 AM
We see so many patterns around us in our daily life. We know that a pattern is an arrangement of objects, colors, or numbers placed in a certain order. Some patterns neither grow nor reduce but only r… -
Patterns in Math | Missing Number | Counting Numbers | Worksheets
Dec 13, 24 12:31 AM
Finding patterns in math is very important to understand the sequence in the series. We need to find the exact missing number that from the group of numbers. The counting numbers may be counting -
Concept of Pattern | Similar Patterns in Mathematics | Similar Pattern
Dec 12, 24 11:22 PM
Concept of pattern will help us to learn the basic number patterns and table patterns. Animals such as all cows, all lions, all dogs and all other animals have dissimilar features. All mangoes have si… -
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 12, 24 10:31 PM
2nd grade geometry worksheet -
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM
What are the different types of lines? There are two different kinds of lines. (i) Straight line and (ii) Curved line. There are three different types of straight lines. (i) Horizontal lines, (ii) Ver…
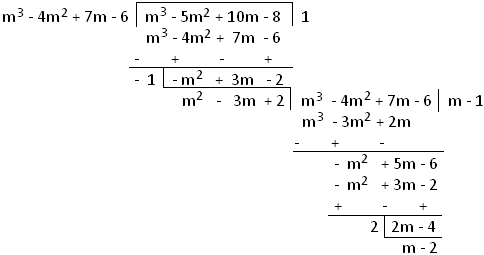
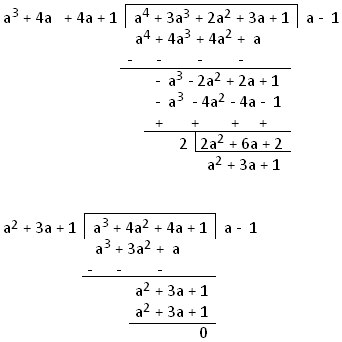
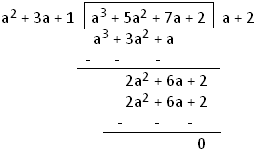
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.