Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Graph of Standard Linear Relations Between x, y
Here we will learn how to draw the graph of standard linear relations between x, y
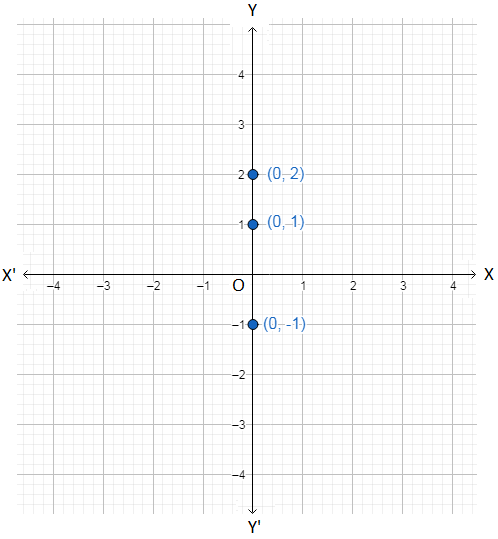
(i) Graph of x = 0
Some of the orders pairs of values of (x, y) satisfying x = 0 are (0, 1), (0, 2), (0, -1), etc.
All the points corresponding to these ordered pairs are on the y-axis because their x-coordinates are 0. Thus,
the graph of x = 0 is the y-axis
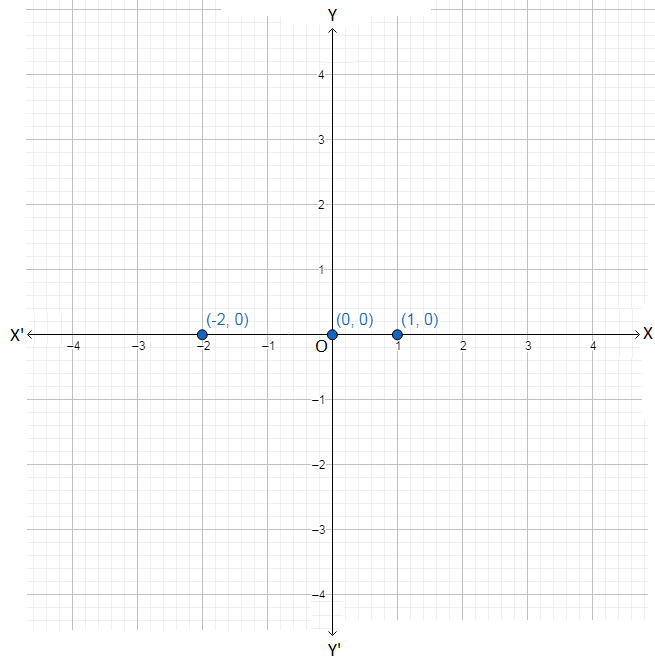
(ii) Graph of y = 0
Some of the ordered pairs of values of (x, y) satisfying y = 0 are (0, 0), (1, 0), (-2, 0), etc.
All these points are on the x-axis, their y-coordinates
being 0.
Thus,
the graph of y = 0 is the x-axis
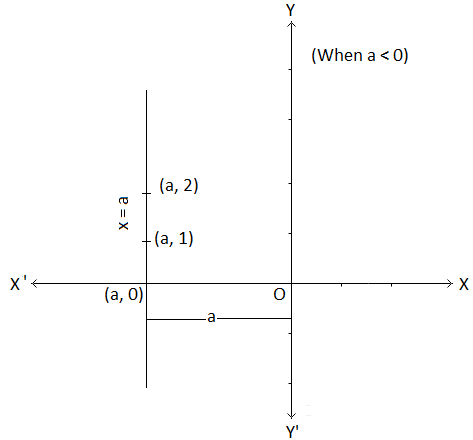
(iiI) Graph of x = a
Some of the ordered pairs of values of (x, y) satisfying x = a are (a, 0), (a, 1), (a, 2), etc.
All these points have the same x-coordinate, a. Plotting these points and joining them by a straight line we get the graph of x = a. We find that
the graph of x = a is a straight line parallel to y-axis at a distance a from the y-axis, on the right if a > 0 and on the left if a < 0.
(iv) Graph of y = a.
Some of the ordered pairs of values (x, y) satisfying y = a are (0, a), (1, a), (3, a), etc.
All these points have the same y-coordinate, a. Plotting these points and joining them by a straight line we get the graph of y = a. We find that
the graph of y = a is a straight line parallel to x-axis at a distance a from the x-axis, above the x-axis if a > 0 and below the x-axis if a < 0.
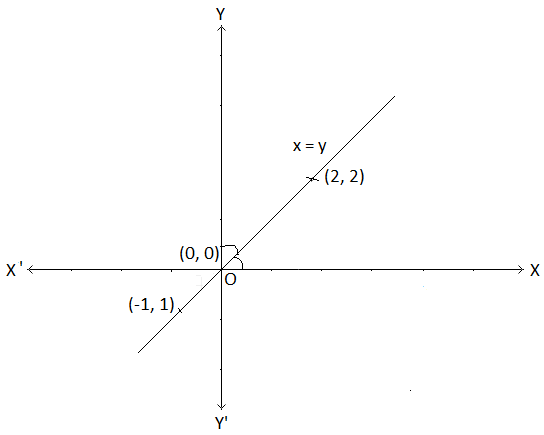
Graph of y = x
Some of the ordered pairs of values of (x, y) satisfying y = x are (0, 0), (-1, -1), (2, 2) etc. All these points have equal x and y coordinates.
So, the points are at equal distances from both the x-axis and y-axis and are in the first quadrant or the third quadrant. Thus,
the graph of y = x is the internal bisector of the angle XOY
From Graph of Standard Linear Relations Between x, y to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
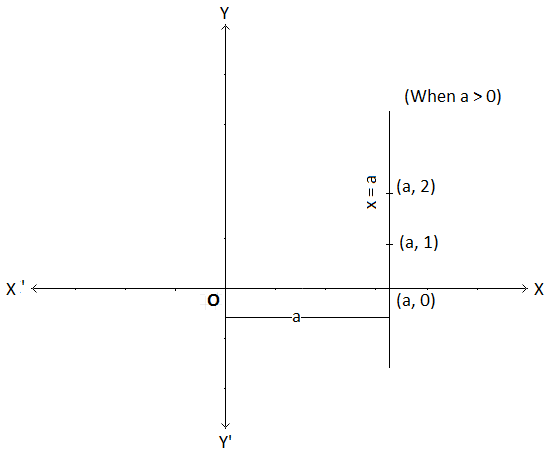
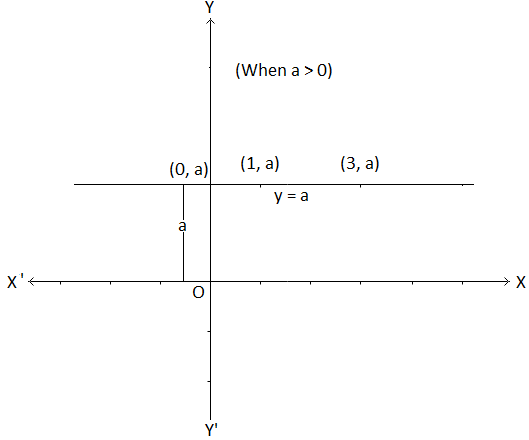
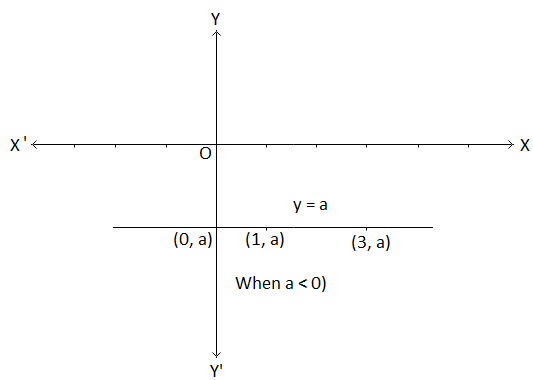


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.