Division in Terms of Reciprocal

We will learn division in terms of reciprocal.

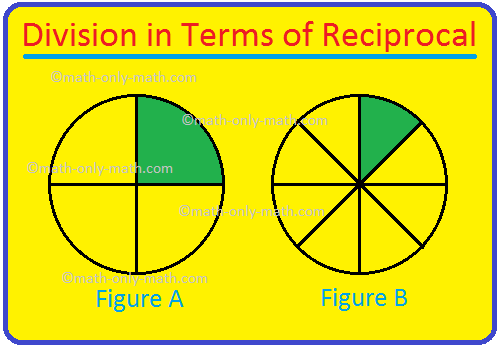
Let us divide \(\frac{1}{4}\) into 2 parts. In the following figure A the colored part represents \(\frac{1}{4}\) of the whole figure. Now, we divide each part into two equal parts. The colored part in the figure B represents \(\frac{1}{8/}\).

Therefore, \(\frac{1}{4}\) ÷ 2 is equal to \(\frac{1}{8}\). We know that the reciprocal or the multiplicative inverse of 2 is \(\frac{1}{2}\).

So, if we multiply \(\frac{1}{4}\) by the reciprocal of 2, we get \(\frac{1}{4}\) × \(\frac{1}{2}\) = \(\frac{1}{8}\).

To divide a fraction or a whole number by a fraction or a whole number, we multiply the reciprocal of the divisor.

Solved Examples on Division in Terms of Reciprocal:

1. Divide 15 by \(\frac{3}{7}\)

Solution:

Reciprocal of \(\frac{3}{7}\) is \(\frac{7}{3}\). Thus 15 ÷ \(\frac{3}{7}\) = \(\frac{15}{1}\) × \(\frac{7}{3}\) = \(\frac{105}{3}\) = 35

2. Divide \(\frac{4}{9}\) by 8

Solution:

\(\frac{4}{9}\) ÷ 8 = \(\frac{4}{9}\) ÷ \(\frac{8}{1}\)

          = \(\frac{4}{9}\) × \(\frac{1}{8}\)

          = \(\frac{4}{72}\)

          = \(\frac{1}{18}\)

3. Divide 13\(\frac{3}{5}\) by 13

Solution:

We first convert the mixed number into improper fraction.

13\(\frac{3}{5}\) = \(\frac{13 × 5 + 3}{5}\) = \(\frac{68}{5}\)

Now, \(\frac{68}{5}\) ÷ 13 = \(\frac{68}{5}\) ÷ \(\frac{13}{1}\)

                     = \(\frac{68}{5}\) × \(\frac{1}{13}\)

                     = \(\frac{68}{65}\)

                     = 1\(\frac{3}{65}\)

4. Divide 4\(\frac{1}{2}\) by \(\frac{3}{4}\)

Solution:

We first convert the mixed number into improper fraction.

4\(\frac{1}{2}\) = \(\frac{4 × 2 + 1}{2}\) = \(\frac{9}{2}\)

Now, \(\frac{9}{2}\) ÷ \(\frac{3}{4}\) = \(\frac{9}{2}\) × \(\frac{4}{3}\)

                   = \(\frac{36}{6}\)

                   = 6

5. How many pieces measuring \(\frac{5}{6}\) m can be cut from a thread of length 150 m?

Solution:

Length of one piece = \(\frac{5}{6}\) m

Length of the thread = 150 m

Number of pieces = 150 ÷ \(\frac{5}{6}\)

                          = 150 × \(\frac{6}{5}\)  

                          = 180

Questions and Answers on Division in Terms of Reciprocal:

I. Fill in the blanks:

(i) \(\frac{3}{16}\) ÷ 1

(ii) \(\frac{8}{15}\) ÷ \(\frac{15}{8}\)  

(iii) \(\frac{5}{9}\) ÷ \(\frac{1}{9}\)  

(iv) \(\frac{3}{10}\) ÷ \(\frac{12}{10}\)  

(v) 5 ÷ \(\frac{20}{7}\)  

(vi) \(\frac{15}{8}\) ÷ 45  

(vii) \(\frac{11}{21}\) ÷ \(\frac{33}{28}\)  

(viii) \(\frac{2}{9}\) ÷ \(\frac{16}{27}\)  

(ix) \(\frac{5}{2}\) ÷ \(\frac{25}{18}\)  

Answers:

(i) \(\frac{3}{16}\)

(ii) \(\frac{64}{225}\)

(iii) 5

(iv) \(\frac{1}{4}\)

(v) \(\frac{7}{4}\)  

(vi) \(\frac{1}{24}\)

(vii) \(\frac{4}{9}\)

(viii) \(\frac{3}{8}\)

(ix) \(\frac{9}{5}\)

II. Word Problems on Division in Terms of Reciprocal:

1. 7\(\frac{1}{2}\) liter of milk has to be packed in bottles of \(\frac{3}{4}\) liters. How many bottles are required to fill all the milk?

Answer: 10 bottles

2. 12\(\frac{1}{2}\) m of cloth is required to stitch 1 shirt. How many shirts can be stitched from a cloth of length 75 m?

Answer: 6 shirts

3. A car covers 30\(\frac{5}{6}\) km in 1 hour. How much time will the car take to cover 360 km?

Answer: 11\(\frac{25}{37}\) hours

4th Grade Math Activities

From Division in Terms of Reciprocal to HOME PAGE