Concept of Decimal

We have already studied about fractions and now we will discuss here about the concept of decimal.

Fractions can also be expressed as decimal Fractions.

We have already studied about fractions. Fractions can also be expressed as decimal Fractions.

\(\frac{1}{10}\) = 0.1

\(\frac{2}{100}\) = 0.02 → Decimal fractions

\(\frac{3}{1000}\) = 0.003

The dot (.) is 0.1, 0.02, 0.003 is called a decimal point or point.

Before we proceed further, let us understand the concept of decimal.

Concept of Decimal

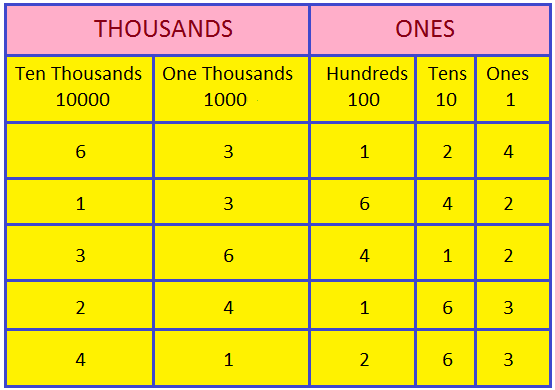
Study the place value chart of the following numerals:

63124, 13642, 36412, 24163, 41263

The place value of 4

in 63124 is  4 ones = 4 × 1 = 4

in 13642 is 4 tens = 4 × 10 = 40

in 36412 is 4 hundreds = 4 × 100 = 400

in 24163 is 4 thousands = 4 × 1000 = 4000

in 41263 is 4 ten thousands = 4 × 10000 = 40000

As the digit moves from right to left

by one place its place value increases 10 times

by two places its place value increases 100 times

by three place its place value increases 1000 times

Observe the place value table shown and note the place value of 1 in each case.

We find that:

Place value of 1 in 8651 = 1 × 1                    = 1

Place value of 1 in 8615 = 1 × 10                 = 10

Place value of 1 in 8165 = 1 × 100               = 100

Place value of 1 in 1865 = 1 × 1000             = 1000

We observe that the place value of a digit is increasing ten times as it moves one place from right to left i.e. the place value of 1 is 1 at ones place, 10 at tens place, 100 at hundreds place and 1000 at thousands place.

Again, observe the table below:

Place value of 1 in 1865 = 1000

Place value of 1 in 8165 = 100

Place value of 1 in 8615 = 10

Place value of 1 in 8651 = 1

We observe that the place value of a digit becomes one tenth as it moves one place from left to right i.e. the place value of 1 is 1000 at thousands place, 100 at hundreds place, 10 at tens place and 1 at ones place. 

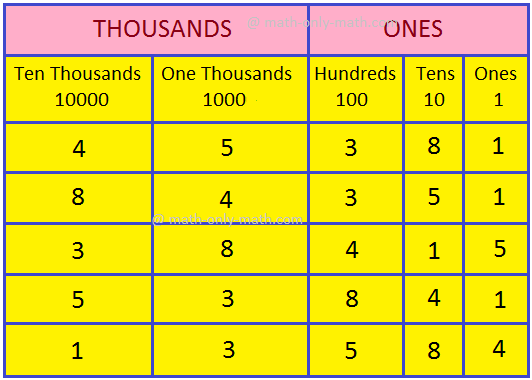
Study the place value chart of the following numerals:

45381,  84351,  38415,  53841,  13584

The place value of 4

in 45381 is  4 ten thousands = 40,000

in 84351 is 4 thousands = 40000 ÷ 10 = 4000

in 38415 is 4 hundreds = 4000 ÷ 10 = 400

in 53841 is 4 tens = 400 ÷ 10 = 40

in 13584 is 4 one = 40 ÷ 10 = 4

As the digit moves from left to right

          by one place, its place value becomes one-tenth [\(\frac{1}{10}\)]

          by two places its place value becomes one-hundredth [\(\frac{1}{100}\)]

          by three place its place value becomes one-thousandth [\(\frac{1}{1000}\)]

A decimal is a fraction whose denominator is 10 or powers of 10.

We can extend the place value chart further as follows:

0.1, 0.01, 0.001 etc. are known as decimal fractions.

We use fractions to express the numbers smaller than 1. We can also express a number smaller than one by using decimal point. Decimal is derived from ‘decem’ the Latin word which means 10. Remember, 10 is the base of the decimal system.

A decimal number consists of two parts – one whole part and one fractional part.

These two are separated by a point called decimal point.

In a decimal the paces occupied by the digits after the decimal point are called decimal places.

Observe the following table:

Picture	Fractional Numbers (for shaded part)	Fractions	Decimals       .	Read as
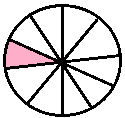
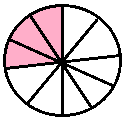
	one-tenth	\(\frac{1}{10}\)	0.1	zero point one
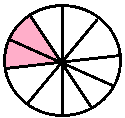
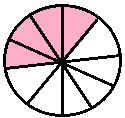
	two-tenths	\(\frac{2}{10}\)	0.2	zero point two
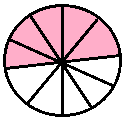
	three-tenths	\(\frac{3}{10}\)	0.3	zero point three
	four-tenths	\(\frac{4}{10}\)	0.4	zero point four
	five-tenths	\(\frac{5}{10}\)	0.5	zero point five

Note: A number without the whole part can be written omitting the zero of the whole part.

For example:

0.1 = .1          0.4 = .4          0.9 = .9 and so on.

A decimal number has two parts - A whole number and a decimal fraction. A decimal point separates them. It is denoted by a dot (.). It is also called point.

Observe the table given below.

Remember, the digits after the point are always read separately. For example, 1.345 is read as one point three four five and not as one point three hundred and forty-five.

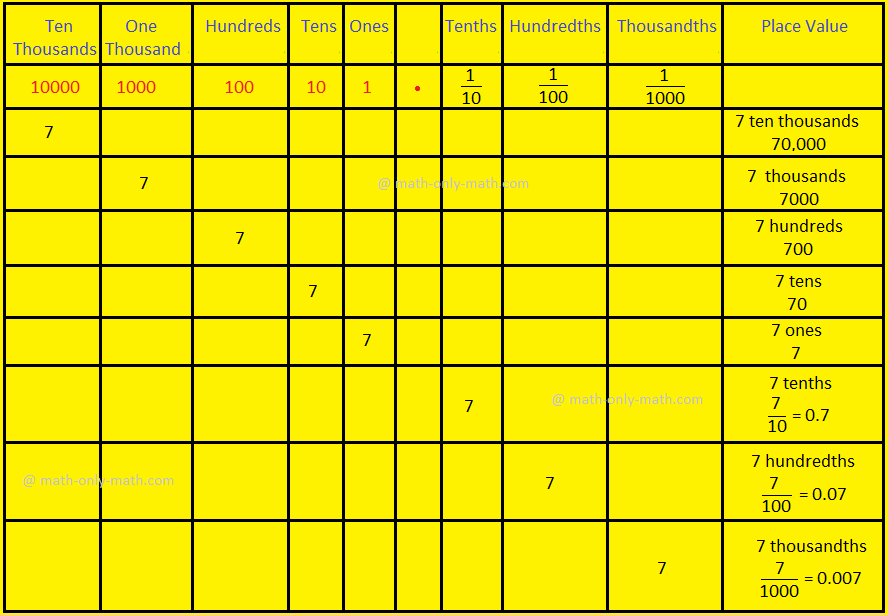
Observe the following place value chart which is extended to tenths, hundredths and thousandths.

When the digit 7 moves one place from the ones place to the right, it is \(\frac{7}{10}\) and read as 7 tenths.

When the digit 7 moves one place from the tenths place to the right, it is \(\frac{7}{100}\) and read as 7 hundredths.

When the digit 7 moves one place from the hundredths place to the right, it is \(\frac{7}{1000}\) and read as 7 thousandths.

Questions and Answers on Concept of Decimals:

I. Write the number names of:

(i) 19.34

(ii) 0.46

(iii) 1.08

(iv) 112.506

(v) 45.245

Answer:

II. Write decimals:

(i) Twenty nine and nine hundredths

(ii) Eighty six and four thousandths

(iii) Five and ninety six hundredths

(iv) One and one thousandth

(v) Seventy five thousandths

III. Write the place value of the underlined digit:

(i) 34.58

(ii) 143.652

(iii) 103.997

(iv) 0.004

(v) 96.829

Answer:

III. (i) 0.5

(ii) 0.002

(iii) 0.007

(iv) 0.004

(v) 0.8

4th Grade Math Activities

From Concept of Decimal to HOME PAGE