Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Comparing Numbers
Comparing numbers is important to know which number is greater and which number is smaller.
We know that, a 2-digit number is greater than a 1-digit number.
Look at the numbers above. They are all written in order.
We observe that 11 is to the left of 12.
Numbers to the left of a number are less than that number.
Look at the numbers again. We observe that 14 is to the right of 13.
Numbers to the right of a number are greater than that number.
Every number is equal to itself.
15 = 15
Look at the numbers above and put the correct sign >, = or < in the boxes.
A: Comparison of 2-Digit Numbers:
How to compare two numbers to find out which is the bigger number.
For example:
1. Compare the numbers 34 and 43.
Method 1: Using the number line
The number that comes later on the number line is the bigger number. First, compare the tens. Then compare the ones.
We know from the number line that 43 comes after 34, so 43 > 34.
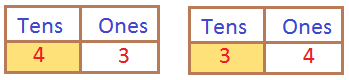
Method 2: Using place value
The number with the greater digit in the bigger place is the bigger number. First, compare the tens. Then compare the ones.
We start with the tens place.
Since 4 > 3 in the tens place, 43 > 34.
2. Compare the numbers 7 and 13.
The number with more number of digits is always greater and the number with less number of digits is always smaller.
7 is a 1-digit number and 13 is a 2-digit number. Therefore, 7 < 13 or 13 > 7.
Note:
What do we do if both the digits are same in the tens place?
We compare the digits in the ones place.
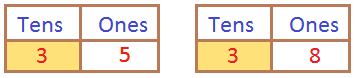
3. Compare the numbers 35 and 38.
Using place value
Step I: First compare the tens place.
The tens place has the digit 3 in both the numbers.
Step II: Then compare the ones place
The ones place has 5 in the number 35.
The ones place has 8 in the number 38.
Since 5 < 8 in the ones place, so 35 < 38 or 38 > 35.
B. Comparison of 3-Digit Numbers:
In the same way a 3-digit number is always greater than a 2-digit number.
The number with more digits is always greater than the number with less digits.
COMPARISON OF NUMBERS
Rules for Comparison
Rule I: If a number has more digits than other, it is greater of the two.
For Example:
Compare the numbers 74 and 248:
Solution:
248 has 3-digits and 74 has 2-digits.
So, by rule-I, 248 is greater than 74, i.e.,
248 74 or 74 < 248.
Rule II: If two numbers have the same number of digits, then
(i) compare the digits on the extreme left. The number with greater digit is greater.
(ii) if the extreme left digits are same, compare the next digits to the right and so on.
For Example:
Compare the numbers:
(a) 973 and 499 (b) 858 and 869 (c) 780 and 789
Solution:
(a) 973 and 499
Both the numbers have 3-digits. But of the two extreme left digits, 9 is greater than 4.
So, by rule II (i) 973 is greater than 499.
i.e., 973 > 499 or 499 < 973.
(b) Both the numbers have 3-digits. Also, extreme left digits are same, namely 8. So, we compare the digits to the right of 8. These digits are 5 and 6.
Since 5 < 6, by rule II (ii), we have: 858 < 869 or 869 > 858.
(c) Both the numbers have 3-digits. The digits at hundreds places are same, namely 7. Also the digits at tens places are same, namely 8.
So, we compare the digits at ones places. These digits are 0 in 780 and 9 in 789.
Since 9 > 0, by rule II (ii), we have: 789 > 780 or 780 < 789.
Note:
To compare two given numbers means to find which of the two numbers is greater or less than the other.
Solved examples for comparing numbers:
1. Let us compare two numbers 103 and 99.
Solution:
103 has 3-digits.
99 has 2-digits.
So, 103 is greater than 99.
2. Compare the number 125 and 87 and find which number is the greater number.
Solution:
1 hundred 2 tens 5 ones = 125 = 12 tens and 5 ones
= 8 tens and 45 ones
8 tens 7 ones = 87 = 8 tens and 7 ones
125 = 8 tens + 45 ones
87 = 8 tens + 7 tens
It is clear 45 ones > 7 ones
or, 125 ones > 87 ones
or, 125 > 87
Therefore, the number which has more digits than the other is greater
If the number of digits are equal, we first compare the digits in hundreds place. The number with greater digit in the hundreds place is greater.
3. Let us compare 369 and 216.
Solution:
Comparing the digits in the hundreds place we find that 3 is greater than 2.
So, 369 is greater than 216 and 369 > 216.
4. Let us compare 468 and 438.
Solution:
Comparing the digits in the hundreds place we find that both numbers have same digit.
Next, we compare the digits in tens place. We find that 6 > 3.
So, 468 > 438
5. Let us compare 822 and 829.
Solution:
Comparing the digits in the hundreds and tens place we find that they are same in both the numbers.
So, we compare the digits in ones place. We find that 9 > 2.
So, 829 > 822.
6. Compare 238
and 148.
Solution:
2 hundred 3 tens 8 ones = 238 = 200 + 30 + 8
1 hundred 4 tens 8 ones = 148 = 100 + 40 + 8
238 = 200 + 30 + 8 = 238 ones
148 = 100 + 40 + 8 =148 ones
It is clear 238 ones > 148 ones.
Hence, 238 > 148 and 148 < 238
Both 238 and 148 have the same number of digits but the digit at hundreds place in 238 has higher place value (200) than the digit at hundreds place value in 148 i.e., (100) or 2 > 1.
Therefore, 238 > 148
7. Compare the following numbers:
(i) 256 and 234
Solution:
2 hundreds + 5 tens + 6 ones = 200 + 50 + 6 = 256 ones
2 hundreds +3 tens + 4 ones =200 + 30 + 4 = 234 ones
256 ones > 234 ones
or, 256 > 234
Both the number have equal number of hundreds, but 256 has more tens 234
Therefore, 256 > 234
(ii) 182 and 186
Solution:
1 hundred + 8 tens + 2 ones = 100 + 80 + 2 = 182 ones
1 hundred + 8 tens + 6 ones = 100 + 80 + 6 = 186 ones
or, 182 < 186
Both the numbers have equal number of hundreds and equal number of tens. But 182 has less ones than 186.
Therefore, 182 < 186
Notes for comparing numbers:
(i) The number having more hundred is greater
(ii) If the number has equal hundreds as the other number, but greater tens than the other, it is greater.
(iii) If one number has equal hundreds and equal tens but more ones than the other, it is greater.
Questions and Answers on Comparing Numbers:
1. Compare the following pairs of numbers and insert > or < sign.
(i) 410 _____ 428
(ii) 362 _____ 381
(iii) 729 _____ 354
(iv) 967 _____ 816
(v) 468 _____ 567
(vi) 637 _____ 691
(vii) 815 _____ 729
(viii) 917 _____ 845
(ix) 752 _____ 672
(x) 711 _____ 237
(xi) 780 _____ 163
(xii) 896 _____ 754
Answer:
1. (i) <
(ii) <
(iii) >
(iv) >
(v) <
(vi) <
(vii) >
(viii) >
(ix) >
(x) >
(xi) >
(xii) >
2. Encircle the smallest number in the group.
(i) 621 852 956 347 446 896
(ii) 217 927 341 789 429 137
(iii) 329 611 328 108 925 423
(iv) 756 157 129 482 128 418
(v) 597 451 516 423 319 616
Answer:
2.(i) 347
(ii) 137
(iii) 108
(iv) 128
(v) 319
3. Colour the box which has the greatest number in the set.
Answer:
3. (i) 456
(ii) 847
(iii) 231
(iv) 481
(v) 760
(vi) 918
(vii) 217
(viii) 359
(ix) 877
4. Colour the box which has the smallest number in the set.
Answer:
4. (i) 437
(ii) 310
(iii) 202
(iv) 237
(v) 716
(vi) 522
(vii) 862
(viii) 221
(ix) 405
5. Compare 65 and 55.
Which is greater?
Answer:
65 is greater than 55
6. Compare 74 and 77.
Which is greater?
Answer:
77 is greater than 74
7. In a train, there are 144 passengers travelling in an air conditioned compartment and 360 passengers are travelling in a non-air conditioned compartment. In which compartment more passengers are travelling? Insert the < or > sign to answer.
Answer:
7. 360 > 144
8. Nitheeya buys 100 stamps less than Joe. If Joe has bought 700 stamps. How many stamps were bought by Nitheeya.
Answer:
8. 600
From Comparing Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.




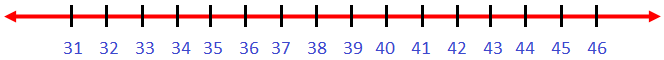





New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.