Constants and Variables

Constants and Variables are the two types of symbols in algebra.

Concept of Constant:

A symbol which has a fixed numerical value is called a constant.

For example:

2, 5, 0, -3, -7, \(\frac{2}{7}\), \(\frac{7}{9}\) etc., are constants.

Number of days in a week represents a constant.

In the expression 5x + 7, the constant term is 7.

Concept of Variables:

In Algebra, letters are used to represent unknown or unspecified numbers. These letters are called variables. Variables are used with plus or minus sign to indicate the addition or subtraction of unspecified numbers.

Definition of Variables: 

A quantity which has no fixed value but takes no various numerical values is called a variable.

For example:

Temperature at different times of a day represents a variable.

The height of a student in your grade is a variable, as it varies from student to student. A variable is denoted by a letter like x, y, z, u, v etc.

A combination of a constant and a variable is also a variable.

The word 'variable' means something that can vary i.e., change, The value of, a variable is not fixed. It can take different values.

For example, in matchstick patterns, the value of 'n' goes on increasing (changing), as a result of which the required number of matchsticks also goes on increasing (changing).

Therefore, 'n' is an example of a variable. Its value is not fixed i.e., it can take any value 1, 2, 3, 4, .... We write the rule for the number of matchsticks required using the variable n.

Use of Variables in Common Rules:

Here, we will see how common rules in mathematics are expressed using variables.

I: Rules From Arithmetic:

1. Commutative Property of Addition of Two Numbers:

Commuting means interchanging Commuting the order of numbers in addition does not change the sum

               i.e., 5 + 4 = 9 and 4 + 5 = 9

               i.e., 5 + 4 = 4 + 5.

The use of variables allows us to express the generality of this property in a concise way.

Let a and b be two variables which can take number of any value. Then, a + b = b + a

Solved Example:

1. Apply the commutative property of addition for the numbers 6 and 9.

Solution:

According to the property, we get 6 + 9 = 15 and 9 + 6 = 15.

Thus, 6 + 9 = 9 + 6 '

Even if the order is changed, the sum remains the same.

This is the commutative property of addition.

2. Commutative Property of Multiplication of Two Numbers:

The order of two numbers being multiplied does not matter. This property of numbers is known as commutative property of multiplication of numbers.

For Example:

5 × 3 = 15 and 3 × 5 = 15

Therefore, 5 × 3 = 3 × 5

Now, using variables a and b, we can also express the commutative property of multiplication of two numbers, such as a × b = b × a.

Solved Example:

1. Apply the commutative property of multiplication for 7 and 3.

Solution:

According to the property, we have 7 × 3 = 21 and 3 × 7 = 21

Thus, 7 × 3 = 3 × 7

This is called commutative property of multiplication.

The product of two numbers is unchanged even if the numbers interchange their places.

3. Distributivity of Numbers:

By using variables, the distributive property can be written in a general and concise way.

Let a, b and c be three variables, each of which can take any number value. Then, the distributive property is given by

                         a(b + c) = ab + ac

Solved Example:

1. Verify the distributive property of multiplication for the numbers 5,  3, 6.

Solution:

We have, 5(3 + 6) = 5 × 9 = 45

5(3 + 6) = (5 × 3) + (5 × 6) = 15 + 30 = 45

Thus, 5(3 + 6) = 5 × 3 + 5 × 6, hence the distributive property of multiplication is verified.

II: Rules From Geometry:

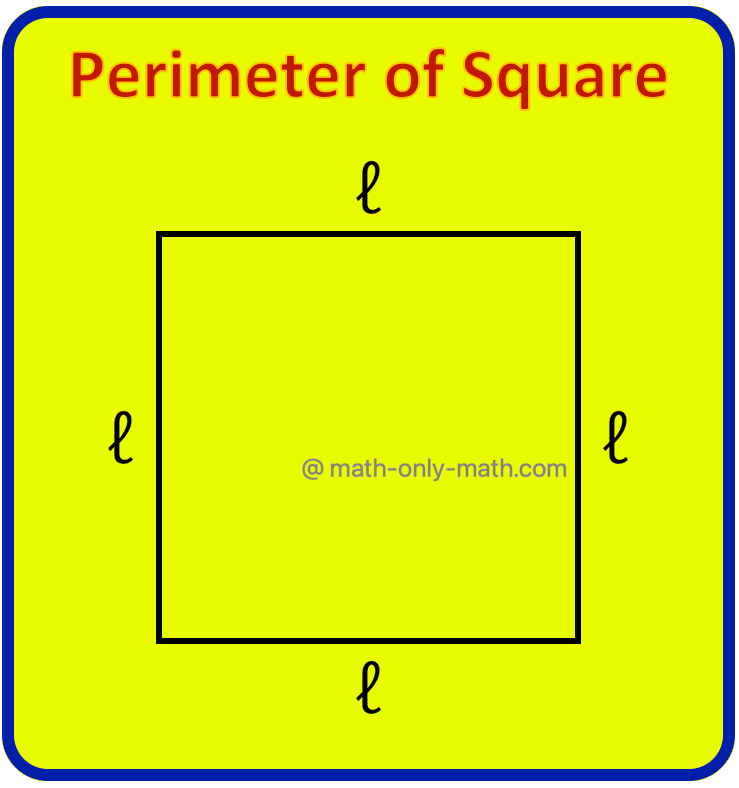
1. Perimeter of Square:

Perimeter of any polygon is the sum of the length of its sides.

A square has sides of equal length.

Perimeter of a square = Sum of lengths of four sides of the square

                                = ℓ + ℓ + ℓ + ℓ

                                = 4 × ℓ

                                = 4ℓ.

Use of the variable ℓ allows us to write the general rule in a way that it is concise and easy to remember.

Perimeter can also be represented by a variable, say p.

Thus, the rule for the perimeter of a square is expressed as a relation between the perimeter and the length of the square i.e., p = 4ℓ.

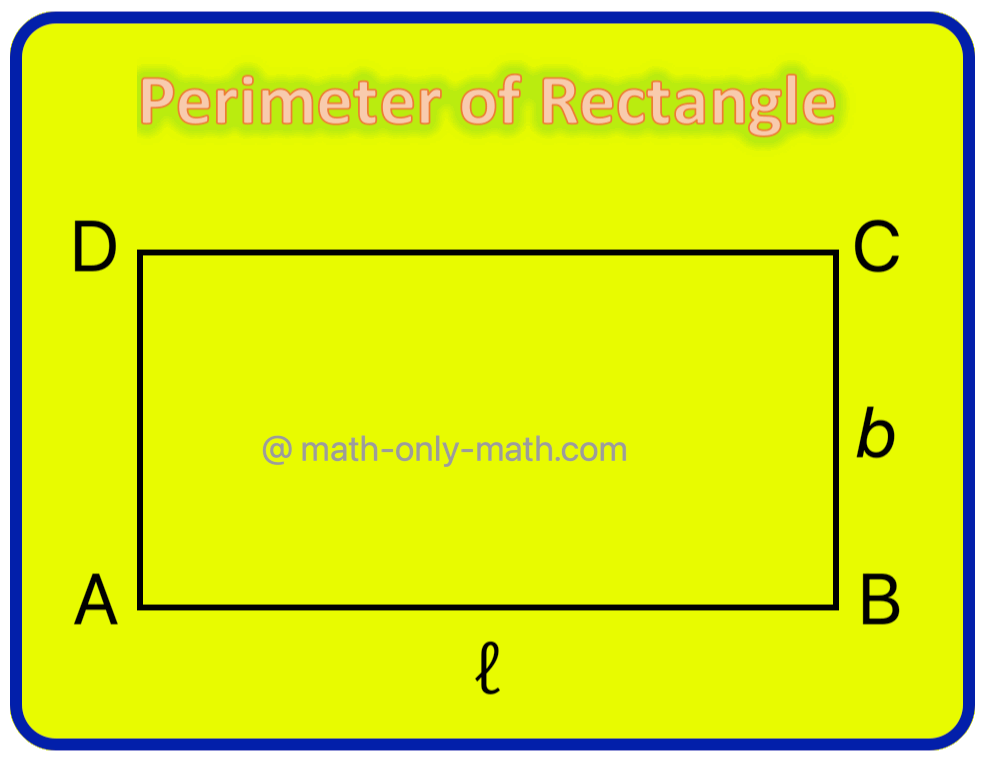
2. Perimeter of Rectangle:

A rectangle has four sides. 

As the opposite sides of rectangle are always equal in length, length of the opposite sides (AB or CD) of rectangle ABCD is denoted by ℓ and other opposite side AD or BC by b.

Therefore, perimeter of rectangle ABCD

            = Sum of lengths of AB, BC, CD, DA

            = ℓ + b + ℓ + b

            = ℓ + ℓ + b + b

            = 2ℓ + 2b

Here, ℓ and b are respectively the length and breadth of the rectangle.

If we denote perimeter of the rectangle by the variable p, the rule for perimeter of a rectangle becomes

               p = 2ℓ + 2b = 2 (ℓ + b).

Note:

Here, both ℓ and b are variables. They take on values independent of each other i.e., the value of one variable does not depend on the value of the other variable.

Examples on Constants and Variables:

(i) In 2a, 2 is a constant and a is a variable.

(ii) In -7mn, -7 is a constant and m and n are variables.

(iii) In 3x, 3 is constant and x is variable but together 3x is a variable.

(iv) If 3 is a constant and x is a variable, then 3 + x, 3 - x, \(\frac{3}{x}\), 3x, \(\frac{x}{3}\), etc., are also variables.

So, we conclude that the combination of a constant and a variable is always a variable.

● Constants and Variables - Worksheet

Worksheet on Constants and Variables

Algebra Page

6th Grade Page

From Constants and Variables to HOME PAGE