4th Grade Fractions Worksheet

In 4th grade fractions worksheet we will circle the like fractions, circle the greatest fraction, arrange the fractions in descending order, arrange the fractions in ascending order, addition of like fractions and subtraction of like fractions.

I. Complete the given Magic Square so that the sum of each row and column is same.

II. Cross product of equivalent fraction is __________ .

III. $\frac{1}{2}$ of a day is __________ hours.

IV. The equivalent of $\frac{5}{11}$ with denominator 66 is __________ .

V. The fraction of vowels in the word APPLICATION is __________ .

VI. A bag contains 27 fruits out of which 12 are apples. What fraction of fruits are not apples. __________

VII. $\frac{19}{35}$ + $\frac{4}{35}$ = $\frac{31}{35}$ - $\frac{8}{35}$ = __________

VIII. Write the next 2 fractions in the series.

$\frac{3}{8}$ = $\frac{9}{24}$ = $\frac{15}{40}$ = __________ = __________

IX. Choose the right answer and fill in the blank.

(i) The smallest fraction among the given is __________ .

(a) $\frac{3}{15}$      (b) $\frac{3}{27}$      (c) $\frac{5}{40}$      (d) $\frac{6}{36}$

(ii) The greatest fraction among the given is __________ .

(a) $\frac{4}{32}$      (b) $\frac{7}{49}$      (c) $\frac{2}{22}$      (d) $\frac{16}{32}$

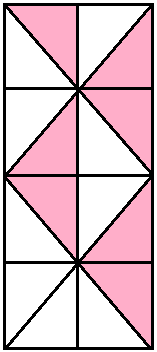
X. Color to show the fraction.

(i) $\frac{1}{2}$

(ii) $\frac{2}{3}$

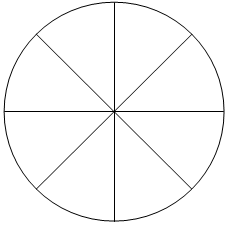
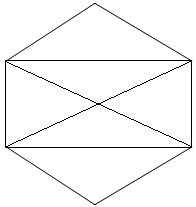
XI. What fraction of the figure is colored?

(i)

(ii)

XII. Circle the like fractions.

(i) $\frac{5}{8}$, $\frac{2}{8}$, $\frac{1}{7}$

(ii) $\frac{2}{15}$, $\frac{6}{7}$, $\frac{11}{15}$

XIII. Circle the greatest fraction.

(i) $\frac{7}{10}$, $\frac{3}{10}$

(ii) $\frac{6}{9}$, $\frac{9}{95}$

XIV. Arrange and write the following in descending order:

(i) $\frac{5}{13}$, $\frac{9}{13}$, $\frac{2}{13}$, $\frac{7}{13}$

XV. Arrange and write the following in ascending order:

(i) $\frac{19}{31}$, $\frac{15}{31}$, $\frac{14}{31}$, $\frac{7}{31}$

XVI. Solve and write the answer.

(i) $\frac{5}{27}$ + $\frac{19}{27}$ =

(ii) $\frac{32}{45}$ - $\frac{17}{45}$ =

XVII. Rebecca bought and filled $\frac{21}{28}$ litres of milk in a can in the morning. By evening $\frac{14}{28}$ litre was left in the can. How much milk was used during the day?

XVIII. Fill in the blanks with correct sign >, < or =.

(i) $\frac{3}{5}$ ……….. $\frac{7}{5}$

(ii) $\frac{8}{9}$ ……….. $\frac{4}{9}$

(iii) $\frac{8}{21}$ ……….. $\frac{12}{21}$

(iv) $\frac{13}{15}$ ……….. $\frac{13}{17}$

(v) $\frac{28}{45}$ ……….. $\frac{28}{39}$

(vi) $\frac{16}{21}$ ……….. $\frac{16}{25}$

(vii) $\frac{1}{3}$ ……….. $\frac{5}{8}$

(viii) $\frac{6}{12}$ ……….. $\frac{14}{28}$

(ix) $\frac{7}{9}$ ……….. $\frac{11}{13}$

XIX. Arrange the given in ascending order.

(i) $\frac{3}{7}$, $\frac{8}{7}$, $\frac{1}{7}$, $\frac{5}{7}$, $\frac{4}{7}$          ____________________

(ii) $\frac{6}{9}$, $\frac{2}{9}$, $\frac{7}{9}$, $\frac{1}{9}$, $\frac{5}{9}$          ____________________

(iii) $\frac{5}{21}$, $\frac{1}{21}$, $\frac{11}{21}$, $\frac{17}{21}$, $\frac{9}{21}$  ____________________

(iv) $\frac{5}{18}$, $\frac{7}{18}$, $\frac{4}{18}$, $\frac{1}{18}$, $\frac{11}{18}$          ____________________

(v) $\frac{6}{17}$, $\frac{2}{17}$, $\frac{5}{17}$, $\frac{4}{17}$, $\frac{1}{17}$          ____________________

XX. Write the given in descending order.

(i) $\frac{7}{19}$, $\frac{4}{19}$, $\frac{13}{19}$, $\frac{3}{19}$, $\frac{18}{19}$          ____________________

(ii) $\frac{17}{42}$, $\frac{3}{42}$, $\frac{9}{42}$, $\frac{11}{42}$, $\frac{7}{42}$  ____________________

(iii) $\frac{6}{11}$, $\frac{2}{11}$, $\frac{7}{11}$, $\frac{9}{11}$, $\frac{4}{11}$          ____________________

(iv) $\frac{3}{22}$, $\frac{5}{22}$, $\frac{9}{22}$, $\frac{6}{22}$, $\frac{13}{22}$          ____________________

(v) $\frac{3}{7}$, $\frac{8}{7}$, $\frac{1}{7}$, $\frac{5}{7}$, $\frac{4}{7}$          ____________________

XXI. Jennifer and Robert are eating a pizza. Jennifer ate $\frac{5}{8}$ pizza and Robert ate $\frac{3}{4}$ pizza. Who ate more pizza? Represent your answer by drawing and coloring the part of pizza in the circles given below.

XXII. Donald and Sandra are driving their cars. Donald covered $\frac{3}{4}$ of the distance in 1 hour and Sandra covered $\frac{5}{8}$ of the distance in one hour. Show travelled in the strips below.

Who is driving fast? What can be the harmful effects of driving very fast?

Answers:

I. $\frac{7}{17}$ 

II. Equal

III. 12

IV. $\frac{30}{66}$ 

V. $\frac{5}{11}$ 

VI. $\frac{15}{27}$ 

VII. $\frac{23}{35}$ 

VIII. $\frac{21}{56}$, $\frac{27}{72}$ 

IX. (i) (b)

(ii) (d)

X.

XI. (i) $\frac{6}{12}$ 

(ii) $\frac{7}{16}$ 

XII. (i) $\frac{5}{8}$, $\frac{2}{8}$ 

(ii) $\frac{2}{15}$, $\frac{11}{15}$ 

XIII. (i) $\frac{7}{10}$ 

(ii) $\frac{9}{9}$ 

XIV. $\frac{9}{13}$, $\frac{7}{13}$, $\frac{5}{13}$, $\frac{2}{13}$ 

XV. (i) $\frac{7}{31}$, $\frac{14}{31}$, $\frac{15}{31}$, $\frac{19}{31}$

XVI. (i) $\frac{24}{27}$

(ii) $\frac{15}{45}$

XVII. $\frac{7}{28}$

XVIII. (i) <

(ii) >

(iii) <

(iv) >

(v) <

(vi) >

(vii) <

(viii) =

(ix) <

XIX. (i) $\frac{1}{7}$, $\frac{3}{7}$, $\frac{4}{7}$, $\frac{5}{7}$, $\frac{8}{7}$ 

(ii) $\frac{1}{9}$, $\frac{2}{9}$, $\frac{5}{9}$, $\frac{6}{9}$, $\frac{7}{9}$ 

(iii) $\frac{1}{21}$, $\frac{5}{21}$, $\frac{9}{21}$, $\frac{11}{21}$, $\frac{17}{21}$

(iv) $\frac{1}{18}$, $\frac{4}{18}$, $\frac{5}{18}$, $\frac{7}{18}$, $\frac{11}{18}$

(v) $\frac{61}{17}$, $\frac{2}{17}$, $\frac{4}{17}$, $\frac{5}{17}$, $\frac{6}{17}$

XX. (i) $\frac{18}{19}$, $\frac{13}{19}$, $\frac{7}{19}$, $\frac{4}{19}$, $\frac{3}{19}$

(ii) $\frac{17}{42}$, $\frac{11}{42}$, $\frac{9}{42}$, $\frac{7}{42}$, $\frac{3}{42}$

(iii) $\frac{9}{11}$, $\frac{7}{11}$, $\frac{6}{11}$, $\frac{4}{11}$, $\frac{2}{11}$

(iv) $\frac{13}{22}$, $\frac{9}{22}$, $\frac{6}{22}$, $\frac{5}{22}$, $\frac{3}{22}$

(v) $\frac{8}{7}$, $\frac{5}{7}$, $\frac{4}{7}$, $\frac{3}{7}$, $\frac{41}{7}$

XXI. Robert

XXII. Donald

4th Grade Math Activities

From 4th Grade Fractions Worksheet to HOME PAGE