Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Relationship between H.C.F. and L.C.M.
We will learn the relationship between H.C.F. and L.C.M. of two numbers.
Relation Between HCF and LCM of Two Numbers:
For two given natural numbers,
(One number) × (Other number) = (Their HCF) × (Their LCM)
This is true only when HCF is a factor of LCM or (HCF)2 is a factor of product of two numbers.
Thus, HCF = \(\frac{\textrm{(One Number) × (Other Number)}}{\textrm{(Their LCM)}}\)
Also, Thus, LCM = \(\frac{\textrm{(One Number) × (Other Number)}}{\textrm{(Their HCF)}}\)
Note: HCF of two numbers is a factor of their LCM.
Let's take the two numbers 15 and 18.
First we need to find the highest common factor (H.C.F.) of 15 and 18 which is 3.
Then we need to find the lowest common multiple (L.C.M.) of 15 and 18 which is 90.
H.C.F. × L.C.M. = 3 × 90 = 270
Also the product of numbers = 15 × 18 = 270
Therefore, product of H.C.F. and L.C.M. of 15 and 18 = product of 15 and 18.
Again, let us consider the two numbers 16 and 24
Prime factors of 16 and 24 are:
16 = 2 × 2 × 2 × 2
24 = 2 × 2 × 2 × 3
L.C.M. of 16 and 24 is 48;
H.C.F. of 16 and 24 is 8;
L.C.M. × H.C.F. = 48 × 8 = 384
Product of numbers = 16 × 24 = 384
So, from the above explanations we conclude that the product of highest common factor (H.C.F.) and lowest common multiple (L.C.M.) of two numbers is equal to the product of two numbers
or, H.C.F. × L.C.M. = First number × Second number
or, L.C.M. = \(\frac{\textrm{First Number} \times \textrm{Second Number}}{\textrm{H.C.F.}}\)
or, L.C.M. × H.C.F. = Product of two given numbers
or, L.C.M. = \(\frac{\textrm{Product of Two Given Numbers}}{\textrm{H.C.F.}}\)
or, H.C.F. = \(\frac{\textrm{Product of Two Given Numbers}}{\textrm{L.C.M.}}\)
For Example:
1. If the LCM of two numbers 180 and 384 is 5760, then find HCF.
Solution:
Here we know the two numbers and their HCF.
We need to find the HCF.
Now using the relation between HCF and LCM of two numbers we get,
HCF = \(\frac{\textrm{(One Number) × (Other Number)}}{\textrm{(Their LCM)}}\)
HCF = \(\frac{\textrm{(180) × (384)}}{\textrm{(5760)}}\)
or, HCF = \(\frac{\textrm{69120}}{\textrm{(5760)}}\)
or, HCF = 12
Hence, the required HCF is 12.
Solved Examples on the
Relationship between H.C.F. and L.C.M.:
1. Find the L.C.M. of 1683 and 1584.
Solution:
First we find highest common factor of 1683 and 1584
Therefore, highest common factor of 1683 and 1584 = 99
Lowest common multiple of 1683 and 1584 = First number × Second number/ H.C.F.
= \(\frac{1584 × 1683}{99}\)
= 26928
2. Highest common factor and lowest common multiple of two numbers are 18 and 1782 respectively. One number is 162, find the other.
Solution:
We know, H.C.F. × L.C.M. = First number × Second number then we get,
18 × 1782 = 162 × Second number
\(\frac{18 × 1782}{162}\) = Second number
Therefore, the second number = 198
3. The HCF of two numbers is 3 and their LCM is 54. If one of the numbers is 27, find the other number.
Solution:
HCF × LCM = Product of two numbers
3 × 54 = 27 × second number
Second number = \(\frac{3 × 54}{27}\)
Second number = 6
4. The highest common factor and the lowest common multiple of two numbers are 825 and 25 respectively. If one of the two numbers is 275, find the other number.
Solution:
We know, H.C.F. × L.C.M. = First number × Second number then we get,
825 × 25 = 275 × Second number
\(\frac{825 × 25}{275}\) = Second number
Therefore, the second number = 75
5. Find the H.C.F. and L.C.M. of 36 and 48.
Solution:
|
H.C.F. = 2 × 2 × 3 = 12 L.C.M. = 2 × 2 × 3 × 3 × 4 = 144 H.C.F. × L.C.M. = 12 × 144 = 1728 Product of the numbers = 36 × 48 = 1728 |
Therefore, product of the two numbers = H.C.F × L.C.M.
6. The H.C.F. of two numbers 30 and 42 is 6. Find the L.C.M.
Solution:
We have H.C.F. × L.C.M. = product of the numbers
6 × L.C.M. = 30 × 42
L.C.M. = \[\frac{30 × 42}{\sqrt{6}}\]
= \[\frac{1260}{\sqrt{6}}\]
= 210
7. Find the greatest number which divides 105 and 180 completely.
Solution:
Therefore, the greatest number that divides 105 and 180 completely is 15.
8. Find the least number which leaves 3 as remainder when divided by 24 and 42.
Solution:
|
L.C.M. of 24 and 42 leaves no remainder when divided by the number 24 and 42. L.C.M. = 2 × 3 × 4 × 7 = 168 |
The least number which leaves 3 as remainder is 168 + 3 = 171.
9. Verify that the HCF of 6 and 27 is a factor of the LCM of the same numbers.
Solution:
We get 6 = 2 × 3
27 = 3 × 3 × 3
So, HCF (Highest Common Factor) of 6 and 27 = 3
We know that, LCM (Least Common Multiple) is the product of all the factors taking maximum repetition of any factor.
Therefore, the LCM of 6 and 27 = 2 × 3 × 3 × 3 = 54
Now, let us divide 54 by 3.
54 ÷ 3 = 3 × 18 + 0
Therefore, the HCF of 6 and 27 is a factor of the LCM of 6 and 27. Hence verified.
Note: The HCF of a group of numbers is always a factor of their LCM .
The product of three or more numbers is not equal to the product of their LCM and HCF.
10. Show that the HCF (Highest Common Factor) of 3 and 6 is not greater than either 3 or 6.
Also, show that the LCM (Least Common Multiple) of 3 and 6 is not less than either 3 or 6.
Solution:
The Highest Common Factor (HCF) of 3 and 6 = 3.
Clearly, the HCF of 3 and 6 i.e., 3 is not greater than either 3 or 6.
So, the HCF of 3 and 6 ≤ 2 or 4.
Similarly, the Least Common Multiple (LCM) of 3 and 6 = 6.
Clearly, the LCM of 3 and 6 i.e., 6 is not less than either 3 or 6.
Therefore, the LCM of 3 and 6 ≥ 3 or 6. Hence proved.
Note: The HCF of a group of numbers is not greater than any of the given numbers, whereas their LCM is not less than any of these numbers.
Important Notes:
Two numbers which have only 1 as the common factor are called co-prime.
The least common multiple (L.C.M.) of two or more numbers is the smallest number which is divisible by all the numbers.
If two numbers are co-prime, their L.C.M. is the product of the numbers.
If one number is the multiple of the other, then the multiple is their L.C.M.
L.C.M. of two or more numbers cannot be less than any one of the given numbers.
H.C.F. of two or more numbers is the highest number that can divide the numbers without leaving any remainder.
If one number is a factor of the second number then the smaller number is the H.C.F. of the two given numbers.
The product of L.C.M. and H.C.F. of two numbers is equal to the product of the two given numbers.
Worksheet on Word problems on Relationship between H.C.F. and L.C.M.
1. The H.C.F. of two numbers 20 and 75 is 5. Find their L.C.M.
2. The L.C.M. of two numbers 72 and 180 is 360. Find their H.C.F.
3. The L.C.M. of two numbers is 120. If the product of the numbers is 1440, find the H.C.F.
4. Find the least number which leaves 5 as remainder when divided by 36 and 54.
5. The product of two numbers is 384. If their H.C.F. is 8, find the L.C.M.
6. The HCF and LCM of two numbers are 3 and 14823 respectively. If one of the numbers is 243, find the other.
7. The product of two numbers is 2835 and their HCF is 9. Find their LCM.
8. If the product of the LCM and HCF is 76614 and one of the numbers is 339, find the other number.
9. The LCM of two numbers is 156 and their product is 624. Find their HCF.
10. Can two numbers have 17 as their HCF and 45 as their LCM?
11. Can two numbers have 11 as their HCF and 110 as their LCM?
12. Verify that HCF of 12, 30 and 48 is a factor of LCM of the same numbers.
13. Verify that LCM of 18, 24 and 72 is a multiple of their HCF.
14. Show that the HCF of 18 and 24 is not greater than either 18 or 24.
Also show that the LCM of 18 and 24 is not less than either 18 or 24.
Answer:
1. 300
2. 36
3. 12
4. 113
5. 48
6. 183
7. 315
8. 226
9. 4.
10. LCM is always a multiple of HCF. or, LCM is divisible by HCF.
But here 45 is not divisible by 17 or 45 is not a multiple of 17. So, its not possible.
11. Yes, Since 110 is divisible by 11.
12. HCF of 12, 30 and 48 = 6.
LCM of 12, 30 and 48 = 240.
240 is divisible by 6.
Therefore, HCF of 12, 30 and 48 is a factor of LCM 12, 30 and 48.
13. LCM of 18, 24, 72 = 72
HCF of 18, 24, 72 = 6
Multiple of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, .....
72 is the multiple of HCF
i.e., LCM of 12, 30 and 48 is the multiple of their HCF.
14. Hints: Follow the Solved Examples on the Relationship between H.C.F. and L.C.M question no. 10
Common Multiples.
Least Common Multiple (L.C.M).
To find Least Common Multiple by using Prime Factorization Method.
Examples to find Least Common Multiple by using Prime Factorization Method.
To Find Lowest Common Multiple by using Division Method
Examples to find Least Common Multiple of two numbers by using Division Method
Examples to find Least Common Multiple of three numbers by using Division Method
Relationship between H.C.F. and L.C.M.
Worksheet on H.C.F. and L.C.M.
Word problems on H.C.F. and L.C.M.
Worksheet on word problems on H.C.F. and L.C.M.
From Relationship between H.C.F. and L.C.M. to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
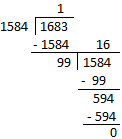


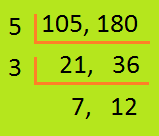
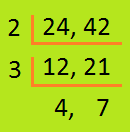


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.