Rationalization
We know that irrational numbers are those which can’t be expressed in the ‘p/q’ form where ‘p’ and ‘q’ are integers. But these rational numbers can be used in rational fractions as either numerator or denominator. When these numbers are present in numerators of fractions, calculations can be done. But when these exist in denominators of fractions, they make calculations more difficult and complicated. To avoid such complications in the numeric calculations, we use method of rationalization. Hence, rationalization can be defined as the process by which we eliminate radicals present in the denominators of fractions.
To understand the concept in a better let us have a look at below solved examples based on rationalization:
1. Rationalization by multiplication of both numerator and denominator by a root:
(i) Rationalize \(\frac{1}{\sqrt{2}}\).
Solution:
Since \(\sqrt{2}\) is a irrational number and is present in denominator of the fraction. So, we first need to rationalize it. This can be done by multiplying both numerator and denominator by \(\sqrt{2}\). So,
\(\frac{1}{\sqrt{2}}\)\(\times\) \(\frac{\sqrt{2}}{\sqrt{2}}\)
⟹ \(\frac{\sqrt{2}}{2}\)
(ii) Rationalize \(\frac{1}{\sqrt{5}}\).
Solution:
Since \(\sqrt{5}\) is a irrational number and is present in denominator of the fraction. So, we first need to rationalize it. This can be done by multiplying both numerator and denominator by \(\sqrt{5}\). So,
\(\frac{1}{\sqrt{5}}\)\(\times\) \(\frac{\sqrt{5}}{\sqrt{5}}\)
⟹ \(\frac{\sqrt{5}}{5}\)
(iii) Rationalize \(\frac{1}{\sqrt{11}}\).
Solution:
Since \(\sqrt{11}\) is a irrational number and is present in denominator of the fraction. So, we first need to rationalize it. This can be done by multiplying both numerator and denominator by \(\sqrt{11}\). So,
\(\frac{1}{\sqrt{11}}\)\(\times\)\(\frac{\sqrt{11}}{\sqrt{11}}\)
⟹ \(\frac{\sqrt{11}}{11}\)
2. Rationalization by multiplication with conjugate.
In the fractions that have irrational numbers in the form of addition or subtraction in the denominators of fraction, we use the method of multiplication with conjugate for rationalizing the fraction and making the problem a simplified.
We have, (x + \(\sqrt{y}\))(x - \(\sqrt{y}\)) = x\(^{2}\) - \((\sqrt{y})^{2}\) = (x\(^{2}\) - y) which is a rational number.
Thus, by multiplying the irrational number (x + \(\sqrt{y}\)) by the irrational number (x - \(\sqrt{y}\)) we get a rational numebr. Here, (x - \(\sqrt{y}\)) is the rationalising factor of (x + \(\sqrt{y}\)). Similarly, (x + \(\sqrt{y}\)) is the rationalising factor of (x - \(\sqrt{y}\)).
The irrational number (x - \(\sqrt{y}\)) is also called the conjugate irrational number, or conjugate, of (x + \(\sqrt{y}\)). Similarly, (x + \(\sqrt{y}\)) is the conjugate of (x - \(\sqrt{y}\)).
For example:
The conjugate of (5 + \(\sqrt{7}\)) is (5 - \(\sqrt{7}\))
The conjugate of (5 - \(\sqrt{7}\)) is (5 + \(\sqrt{7}\))
The conjugate of (10 + \(\sqrt{3}\)) is (10 - \(\sqrt{3}\))
The conjugate of (10 - \(\sqrt{3}\)) is (10 + \(\sqrt{3}\))
Below given are the examples on rationalizing the fractions by multiplying with conjugate:
(i) Rationalize \(\frac{1}{4 + \sqrt{2}}\).
Solution:
Since, the given problem has irrational term in the denominator with addition and subtraction format. So we need to rationalize using the method of multiplication by conjugate. So,
\(\frac{1}{4 + \sqrt{2}}\) \(\times\) \(\frac{4 - \sqrt{2}}{4 - \sqrt{2}}\)
⟹ \(\frac{4 - \sqrt{2}}{4^{2} - \sqrt{2^{2}}}\), [Since, (a + b)(a - b) = a\(^{2}\) - b\(^{2}\)}]
⟹ \(\frac{4 - \sqrt{2}}{16 - 2}\)
⟹ \(\frac{4 - \sqrt{2}}{14}\)
So, the required rationalized number is:
\(\frac{4 - \sqrt{2}}{14}\)
(ii) Rationalize\(\frac{1}{3 - \sqrt{5}}\).
Solution:
Since, the given problem has irrational term in the denominator with addition and subtraction format. So we need to rationalize using the method of multiplication by conjugate. So,
\(\frac{1}{3 - \sqrt{5}}\) \(\times\) \(\frac{3 + \sqrt{5}}{3 + \sqrt{5}}\)
⟹ \(\frac{3 + \sqrt{5}}{3^{2} - \sqrt{5^{2}}}\), [Since, (a + b)(a - b) = a\(^{2}\) - b\(^{2}\)}]
⟹ \(\frac{3 + \sqrt{5}}{9-5}\)
⟹ \(\frac{3 + \sqrt{5}}{4}\)
⟹ So, the required rationalized number is \(\frac{3 + \sqrt{5}}{4}\)
Irrational Numbers
Definition of Irrational Numbers
Representation of Irrational Numbers on The Number Line
Comparison between Two Irrational Numbers
Comparison between Rational and Irrational Numbers
Problems on Irrational Numbers
Problems on Rationalizing the Denominator
Worksheet on Irrational Numbers
From Rationalization to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
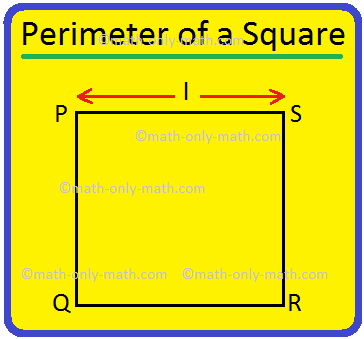
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
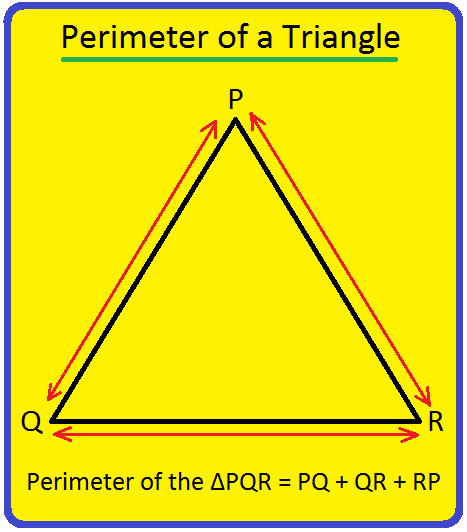
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
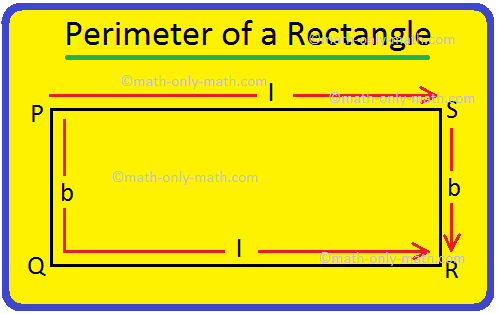
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…