Pyramid

What is pyramid?

A pyramid is a solid bounded by plane faces ; one of its faces is a polygon of any number of sides and the other faces are triangles whose bases are the sides of the polygon and which meet at a common point outside the plane of the polygon.

The plane face which is a polygon is called the base of the pyramid and the triangular faces are its lateral faces. The common point at which the lateral faces meet is called its vertex. The straight lines in which adjacent faces intersect are called the edges (or lateral edges) of the pyramid. The perpendicular distance from the vertex to the plane of the base is called the height (or altitude) of the pyramid. Evidently, a pyramid will have n lateral faces if its base is a polygon of n sides. A pyramid is said to be triangular, quadrangular, pentagonal or hexagonal according as its base is a triangle, quadrilateral, pentagon or hexagon.

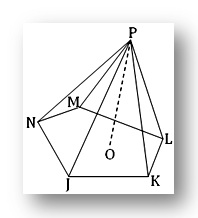
A pyramid has been displayed in given figure. The base of the pyramid is the pentagon JKLMN, its vertex is P; its lateral faces are the plane triangles PJK, PKL etc. and PJ, PK etc. are its edges. If PO be perpendicular to the plane of the base JKLMN then its height is PO.

Right Pyramid: If the base of a pyramid is a regular polygon and perpendicular drawn from its vertex to the base passes through the centre of the base (i.e. the centre the circumscribed or the inscribed circle of the regular polygon) then the pyramid is called a right pyramid.

The lateral faces of a right pyramid are congruent isosceles triangles. The length of the line joining the vertex to the centre of the base is called height of the right pyramid. The length of the perpendicular drawn from the vertex to any side of base is called the slant height of the right pyramid. Evidently, the slant height is the same for each lateral face of a right pyramid and each slant height bisects the corresponding side of the base. The sum of the areas of the lateral faces of a right prism is called its slant surface.

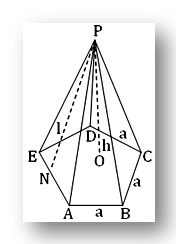
A right pyramid has been shown in the given figure. It’s base is the regular pentagon ABCDE and P is its vertex; PO is the height of the right pyramid, P0 being the centre of the base; PAB, PBC etc. are its lateral faces which are all isosceles triangles having equal area. If PN bisects AE at right angles, then PN is the slant height of the right pyramid.





Let a be the length of each side of the base of a right pyramid. If h be the height and 1, the slant height of the right pyramid, then

1. The area of the slant surface of the right pyramid

= 1/2 a ∙ l + 1/2 a ∙ l + 1/2 a ∙ l + ……..

= 1/2 ( a + a + a + ……) ∙ l

= 1/2 × perimeter of the base × slant height;

2. Area of whole surface of the right pyramid = area of its slant surface + i.e. area of its base

3. Volume of a right pyramid = 1/3 × area of the base × height.

● Mensuration

• Formulas for 3D Shapes
  
• Volume and Surface Area of the Prism
  
• Worksheet on Volume and Surface Area of Prism
  
• Volume and Whole Surface Area of Right Pyramid
  
• Volume and Whole Surface Area of Tetrahedron
  
• Volume of a Pyramid
  
• Volume and Surface Area of a Pyramid
  
• Problems on Pyramid
  
• Worksheet on Volume and Surface Area of a Pyramid
  
• Worksheet on Volume of a Pyramid

11 and 12 Grade Math 

From Pyramid to HOME PAGE