Pairs of Equations
Solving pairs of equations, indicate the pair or pairs representing simultaneous linear equations (solvable).
1. From the following pairs of equations find the pair or pairs representing simultaneous equations:
(i) 7x – 3y = 5
2x + 5y = 1
Solution:
7/2 ≠ -3/5, so the two equations represent simultaneous equations; in this case they have only one solution.
(ii) 2x + 3y = 7
6x + 9y = 11
Solution:
2/6 = 3/9 ≠ 7/11
Not simultaneous equations.
(iii) 6x - 4y = 8
3x - 2y = 4
Solution:
6/3 = -4/-2 = 8/4
Simultaneous equations; have infinite solutions.
2. For which value of k, kx + y = 2 and x + ky = 1 are inconsistent?
Solution:
The two equations will be inconsistent if k/1 = 1/k ≠ 2/1 that means, k² = 1 or k = ±1
Therefore, the two given equations will be inconsistent if k = ±1
3. If solvable, solve the following pairs of equations:
(i) 3x – 2y = 1
3x + 2y = 5
Solution:
Here, comparing co-efficient of x and y, we get;
3/3 ≠ -2/2
Therefore, adding the two equations, we get the general solution as shown below:
6x = 6
or, x = 1
Putting x = 1 in the first equation we get:;
3 × 1 – 2y = 1
or, 3 - 2y = 1
or, 3 – 3 – 2y = 1 – 3
or, -2y = -2
or, y = 1
Therefore, the required solution: x = 1, y = 1
(ii) 3x – 2y = 1
6x – 4y = 8
Solution:
Here, comparing the co-efficient of x, y we get;
3/6 = -2/-4 ≠ 1/8
So, the two equations have no general solution.
(iii) 3x – 2y = 2
9x – 6y = 6
Solution:
Comparing co-efficient of x, y and the term free from x, y we get;
3/9 = -2/-6 = 2/6
Therefore, two equations are, in fact, same.
Assuming x = c in 3x – 2y = 2 we get;
y = (3c – 2)/2
Therefore, required solution: x = c
y = (3c – 2)/2 for any real value of c.
● Simultaneous Linear Equations
Solvability of Linear Simultaneous Equations
Word Problems on Simultaneous Linear Equations
Word Problems on Simultaneous Linear Equations
Practice Test on Word Problems Involving Simultaneous Linear Equations
● Simultaneous Linear Equations - Worksheets
Worksheet on Simultaneous Linear Equations
Worksheet on Problems on Simultaneous Linear Equations
8th Grade Math Practice
From Pairs of Equations to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Pictograph to Represent The Collected Data | Forming Pictograph | Math
May 07, 24 05:36 PM
Pictures or symbols are made in a pictograph to represent the collected data. So, we can say that a pictograph represents the data and gives information quickly and clearly. -
Examples of Pictographs |Pictorial Representation|Pictograph Questions
May 07, 24 05:27 PM
Some sample examples of pictographs or pictorial representation are shown, how the objects are used to give information regarding mathematical data. Read the pictograph and gather the information -
Mental Math on Time | 4th Grade Time Worksheet | Tricks | Techniques
May 07, 24 01:36 PM
In mental math on time, we will solve different types of problems on reading time to the nearest minutes, reading time to the exact minutes, use of a.m. and p.m., 24-hours clock, days in a year and ca… -
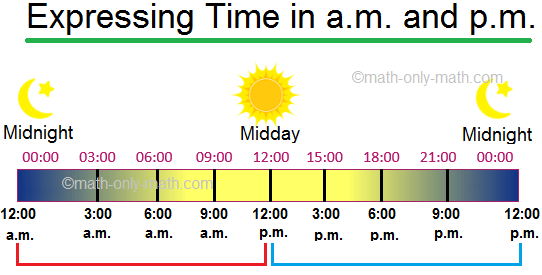
Telling Time in a.m. and p.m. | Antemeridian and Postmeridian|Examples
May 06, 24 05:54 PM
The clock shows time in 12 hour cycle. The first cycle of the hour hand completes at 12 o’clock midday or noon. The second cycle of the hour hand completes at 12 o’clock midnight. ‘a.m.’ and ‘p.m.’ ar… -
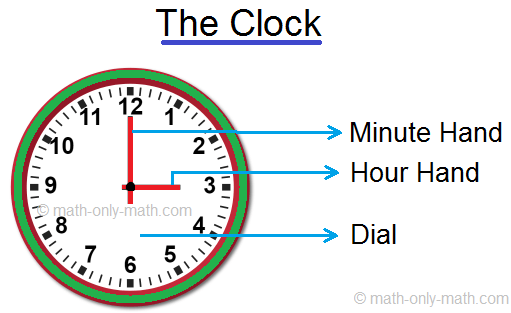
Different Ways of Reading Time | Many Ways to Read Time | Telling Time
May 06, 24 05:23 PM
What are the different ways of reading time? There are many ways to read time: (a) When hour-hand is exactly at any number and minute-hand is at 12, we read the time in full hours. If hour hand is at



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.