Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Mark-ups and Discounts Involving Sales Tax
We will discuss here how to solve the problems based on mark-ups and discounts involving sales tax.
1. Davis bought a car listed at $ 536500 at 8% discount and then 10% sales tax charged on the discounted price. Find the amount Davis paid for the car.
Solution:
Price listed on the car = $ 536500, rate of discount = 8%
Therefore, the amount of discount = $ (536500 X 8/100) = $ 42920
Therefore, the selling price of the car = $ (536500 - 42920) = $ 493580.
The rate of sales tax = 10%
Therefore, the sale tax on the car = $ (493580 X 10/100) = $ 49358
Therefore, the amount paid by Davis = $ (493580 + 49358) = $ 542938.
2. Ron buys a car for $ 38,400 which includes 10% discount
and then 6% sales tax on the marked price. Find the marked price of the car.
Solution:
Let the marked price of the car be P. Then, the discount on marked price = 10% of P = 10/100 P = P/10, and sales tax = 6% of P = 6/100 P = 3P/50
Therefore, the price paid = P – P/10 + 3P/50 = 50P – 5P + 3P/50 = 48P/50 = 24P/25
According to the problem we get, 24P/25 = $38400
P = $38400 × 25/24
= $1600 × 25
= $40000
Therefore, the marked price of the car is $40000.
3. Due to short supply in the market, a shopkeeper raises the price of a cycle by 5% above the marked price and charges a sales tax of 12 % on the marked price. A customer has to pay $ 4680 for the cycle. Find the marked price of the cycle.
Solution:
Let the marked price of a cycle be P.
Then, the raised price = P + 5% of P = P + 5P/100 = 21P/20
Sales tax = 12% of P = 12/100 P = 3/25 P
Therefore, the price payable = 21P/20 + 3P/25 = 105P + 12P/100 = 117P/100
According to the problem we get, 117P/100 = $4680
P = $4680 × 100/117
= $4000
Therefore, the marked price of the cycle is $4000.
4. Jack buys a laptop for $ 34821 which includes 10% rebate on the listed price and then 6% sales tax on the remaining price. Find the listed price of the computer.
Solution:
Let the listed price of the laptop be $ x, rebate on the listed price = 10%
Therefore, the amount of rebate = $ (x + 10/100) = $ x/10
Therefore, cost of the laptop after rebate = $ x - $ x/10 = $ 9/10 x
Since sale tax is 6% on the remaining price,
Therefore, the amount of sales tax= $ 9/10x X 6/100 = $ 27/500 x.
Therefore, the net amount to be paid = $ 910x + $ 27/500 x
= $(9/10x + 27/500x)
According to the problem, we get,
9/10x +27/500x = 34821
Or, 477/500x = 34821
Or, x = 36500.
Therefore, the marked price of the laptop = $ 36500.
● Sales Tax and Value Added Tax
- Calculation of Sales Tax
- Sales Tax in a Bill
- Mark-ups and Discounts Involving Sales Tax
- Profit Loss Involving Tax
- Value Added Tax
- Problems on Value Added Tax (VAT)
- Worksheet on Printed Price, Rate of Sales Tax and Selling Price
- Worksheet on Profit/Loss Involving Sales Tax
- Worksheet on Sales Tax and Value-added Tax
- Worksheet on Mark-ups and Discounts Involving Sales Tax
10th Grade Math
From Mark-ups and Discounts Involving Sales Tax to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
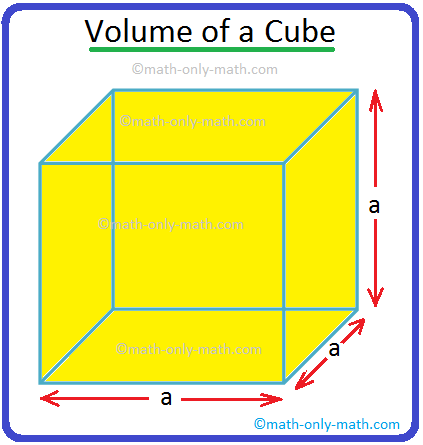
Volume of a Cube | How to Calculate the Volume of a Cube? | Examples
Jul 22, 25 03:02 PM
A cube is a solid box whose every surface is a square of same area. Take an empty box with open top in the shape of a cube whose each edge is 2 cm. Now fit cubes of edges 1 cm in it. From the figure i… -
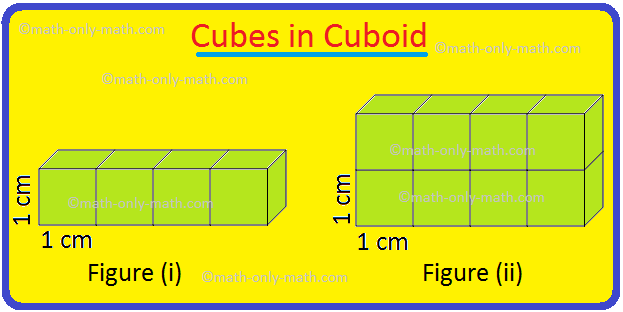
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 20, 25 12:58 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on… -
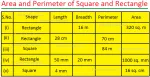
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
Jul 19, 25 05:00 AM
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square len… -
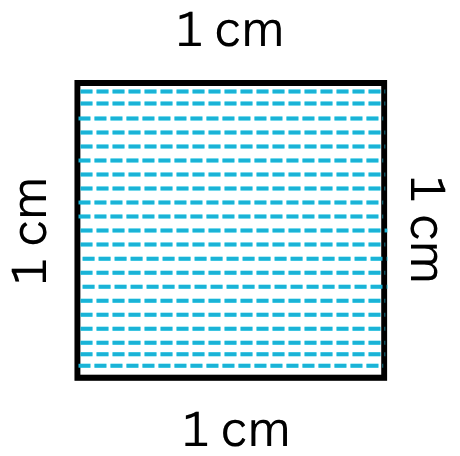
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for…


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.