Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Volume of Cube
Here we will learn how to solve the application problems on Volume of cube using the formula.
Formula for finding the volume of a cube
Volume of a Cube (V) = (edge)3 = a3;
where a = edge
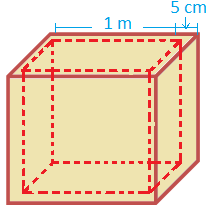
1. A cubical wooden box of internal dimensions 1 m × 1 m × 1 m is made of 5 cm thick wood. The wood costs Rs. 18600 per cubic metre. If the box is open at the top, find the cost of wood required for making the box.
Solution:
Clearly, the outer dimensions of the box are as follows
The outer length = 1 m + 2 × 5 cm = 1.10 m
The outer breadth = 1 m + 2 × 5 cm = 1.10 m
The outer height = Inner height + 5 cm (since, the box is open at the top)
= 1.05 m
Therefore, the volume of wood required = Volume of the outer cuboid - volume of the inner cube
= 1.10 × 1.10 × 1.05 m3 - 13m3
= 1.2705 m3 - 1 m3
= 0.2705 m3
Therefore, the cost of wood = 0.2705 × Rs. 18600
= Rs. 5031.30
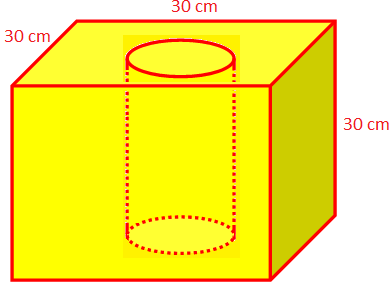
2. The edge of a cubical block of wood measures 30 cm. A straight cylindrical hole of diameter 10 cm is drilled through the cube. Find the volume of the wood left in the block.
Solution:
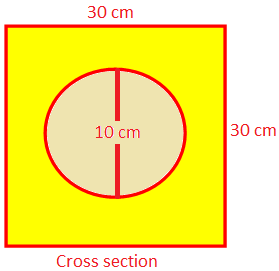
Are of the cross section of the wood block left = Area of a face of the cube of edge 30 cm - Area of a circle of diameter 10 cm.
= {302 - π ∙ (\(\frac{10}{2}\))2} cm2
= (900 - 25π) cm2.
Therefore, the volume of the wood left = (Are of the cross section) × Height
= (900 - 25π) × 30 cm3.
= (27000 - 750 × \(\frac{22}{7}\)) cm3.
= \(\frac{172500}{7}\) cm3.
= 24,642\(\frac{6}{7}\)cm3.
From Volume of Cube to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.