Two Tangents from an External Point
Here we will prove that from any point outside a circle two tangents can be drawn to it and they are equal in length.
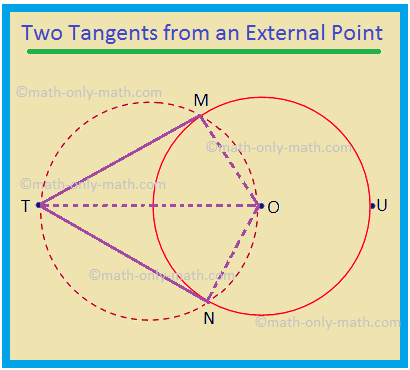
Given: O is the centre of a circle and T is a point outside the circle.
Construction: Join O and T. Draw a circle with TO as diameter which cuts the given circle at M and N. Join T to M and N.
To prove: TM and TN are tangent to the circle and TM = TN.
Proof:
|
Statement |
Reason |
|
1. ∠TMO = 90°. |
1. Angle in a semicircle is a right angle. |
|
2. TM ⊥ OM. |
2. From statement 1. |
|
3. Therefore, TM is a tangent to the given circle. |
3. Tangent ⊥ radius drawn through point of contact. |
|
4. Similarly, TN is a tangent to the given circle. |
4. Proceeding as above. |
|
5. In ∆TOM and ∆TON, (i) OM = ON. (ii) ∠OMT = ∠ONT = 90°. (iii) TO = TO. |
5. (i) Radii of the same circle. (ii) Radius ⊥ tangent. (iii) Common side. |
|
6. ∆TOM ≅ ∆TON. |
6. By RHS criterion. |
|
7. TM = TN. |
7. CPCTC. |
Note:
1. The two tangents subtend equal angles at the centre of the circle.
∠TOM = ∠TON, as ∆TOM ≅ ∆TON.
2. The two tangents are equally inclined to the line joining the point to the centre of the circle.
∠MTO = ∠NTO, as ∆TOM ≅ ∆TON.
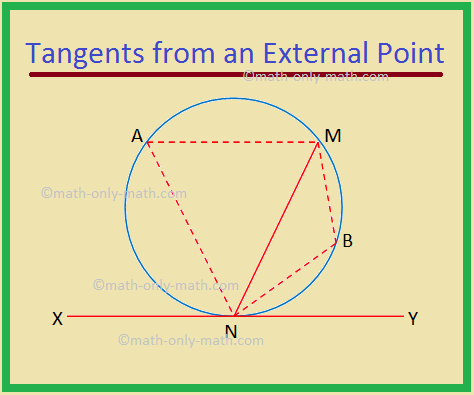
Alternate Segments
In the given below figure, the chord MN divides the circle into two segments. The tangent XY is drawn that touches the circle N.
The alternate segment for ∠MNY is the segment MAN and that for ∠MNX is the segment MBN.
The angle in the alternate segment for ∠MNY is ∠MAN and that for ∠MNX is ∠MBN.
From Two Tangents from an External Point to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Converting Fractions to Decimals | Solved Examples | Free Worksheet
Apr 28, 25 01:43 AM
In converting fractions to decimals, we know that decimals are fractions with denominators 10, 100, 1000 etc. In order to convert other fractions into decimals, we follow the following steps: -
Expanded Form of a Number | Writing Numbers in Expanded Form | Values
Apr 27, 25 10:13 AM
We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its… -
Converting Decimals to Fractions | Solved Examples | Free Worksheet
Apr 26, 25 04:56 PM
In converting decimals to fractions, we know that a decimal can always be converted into a fraction by using the following steps: Step I: Obtain the decimal. Step II: Remove the decimal points from th… -
Worksheet on Decimal Numbers | Decimals Number Concepts | Answers
Apr 26, 25 03:48 PM
Practice different types of math questions given in the worksheet on decimal numbers, these math problems will help the students to review decimals number concepts. -
Multiplication Table of 4 |Read and Write the Table of 4|4 Times Table
Apr 26, 25 01:00 PM
Repeated addition by 4’s means the multiplication table of 4. (i) When 5 candle-stands having four candles each. By repeated addition we can show 4 + 4 + 4 + 4 + 4 = 20 Then, four 5 times
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.