Triangular Numbers Pattern
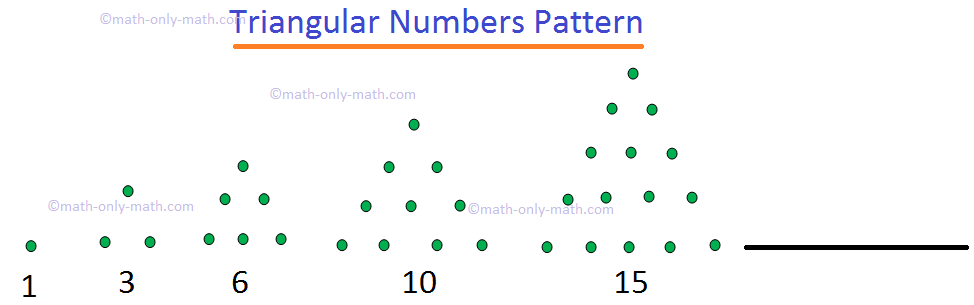
Let us consider the following series of numbers. 1, 3, 6, 10, 15, 21, ….
If we represent each number of above series by a dot and arrange them in such a way that they make a triangle. Such numbers are known as triangular numbers.
Look at the following arrangements of dots.
The triangular numbers are 1, 3, 6, 10, 15, 21, 28, 36, …
The rule to find the triangular number in a series is:
First term = 1
Second term = First term + 2
Third term = Second term + 3
Fourth term = Third term + 4 and so on.
Examples on Triangular Numbers Pattern:
1. Find the next triangular number in the series 45, 55, …
Solution:
The difference of two terms = 55 – 45 = 10
To get the next term we add 1 more to the previous term difference = 10 + 1 = 11
The next term is 55 + 11 = 66
Questions and Answers on Triangular Numbers Pattern:
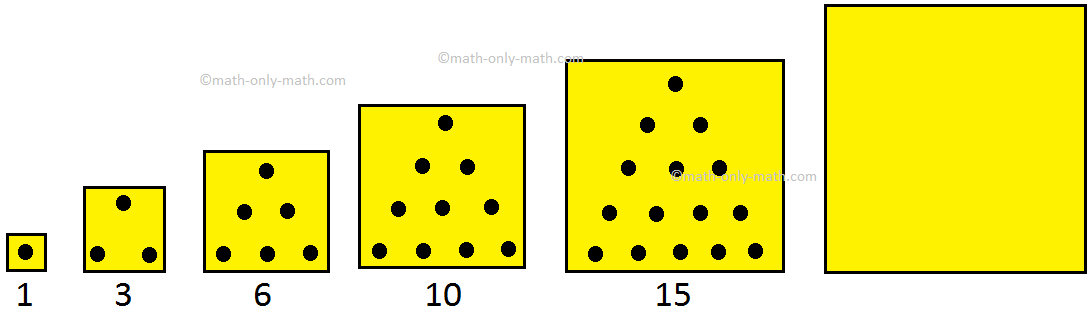
I. Given below is a triangular pattern. The dots on each side are same. Draw appropriate number of dots in the empty box to get the next figure of the pattern.
Answer:
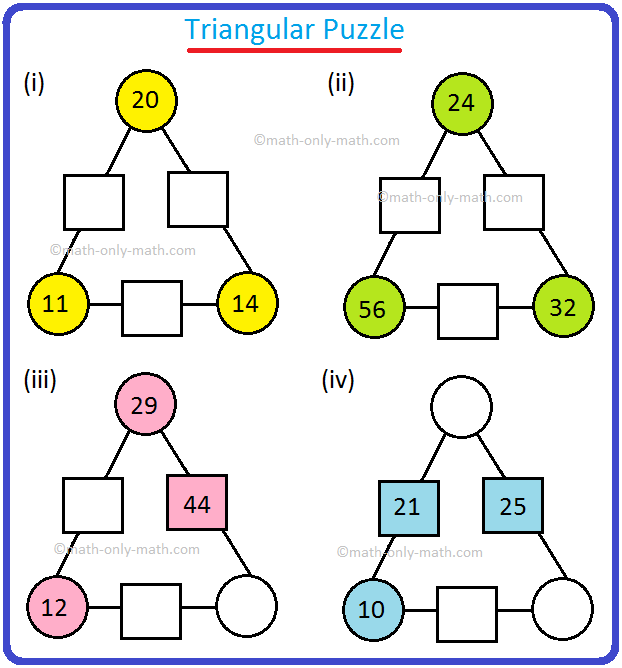
II. In the
given triangular puzzle, the numbers in the circle add together to make the
number in the rectangle. Find the missing numbers in the puzzle.
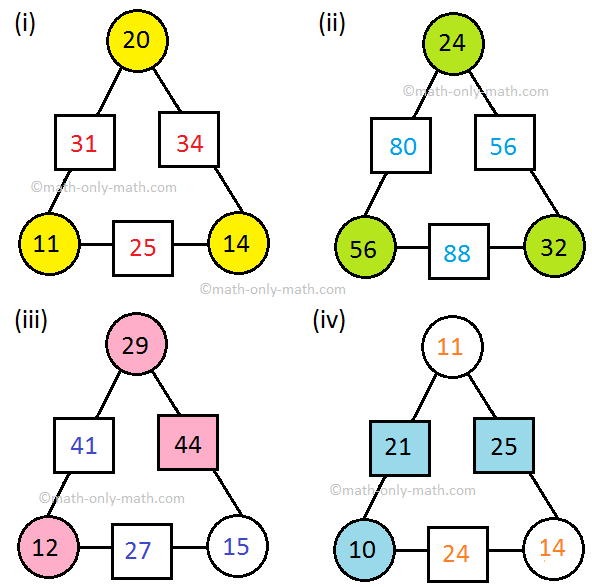
Answer:
III. Write the next 3 numbers of the triangular series.
1, 3, 6, 10, 15, 21, ……., ……., …….
Answer:
28, 36, 45
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.