Riders Based on Pythagoras’ Theorem

Here we will solve different types of examples on establishing riders based on Pythagoras’ theorem.

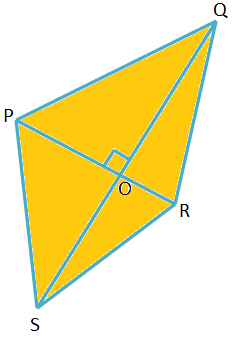
1. In the quadrilateral PQRS the diagonals PR and QS intersects at a right angle. Prove that PQ²+ RS² = PS² + QR².

Solution:

Let the diagonals intersect at O, the angle of intersection being a right angle.

In the right-angle ∆POQ, PQ² = OP² + OQ².

In the right-angle ∆ROS, RS² = OR² + OS².

Therefore, PQ² + RS² = OP² + OQ² + OR² + OS² ................. (i)

In the right-angle ∆POS, PS² = OP² + OS².

In the right-angle ∆QOR, QR² = OQ² + OR².

Therefore, PS² + QR² = OP² + OS² + OQ² + OR² ................. (ii)

From (i) and (ii), PQ²+ RS² = PS² + QR². (Proved).

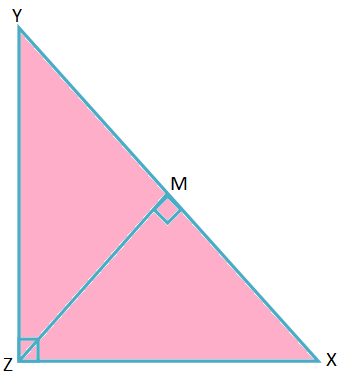
2. In ∆XYZ, ∠Z = 90° and ZM ⊥ XY, where M is the foot of the perpendicular. Prove that $\frac{1}{ZM^{2}}$ = $\frac{1}{YZ^{2}}$ + $\frac{1}{XZ^{2}}$.

Solution:

In ∆XYZ and ∆ZYM,

∠XZY = ∠ZMY = 90°,

∠XYZ = ∠ZYM (Common Angle)

Therefore, by AA criterion of similarity,  ∆XYZ ∼ ∆ZYM.

$\frac{XY}{YZ}$ = $\frac{XZ}{ZM}$

⟹ YZ ∙ XZ = XY ∙ ZM

Therefore, ZM = $\frac{YZ ∙ XZ}{XY}$

Therefore, $\frac{1}{ZM^{2}}$ = $\frac{XY^{2}}{YZ^{2}  ∙  XZ^{2}}$ = $\frac{XZ^{2} + YZ^{2}}{YZ^{2}  ∙  XZ^{2}}$; [By Pythagoras’ theorem)

Therefore, $\frac{1}{ZM^{2}}$ = $\frac{1}{YZ^{2}}$ + $\frac{1}{XZ^{2}}$. (Proved)

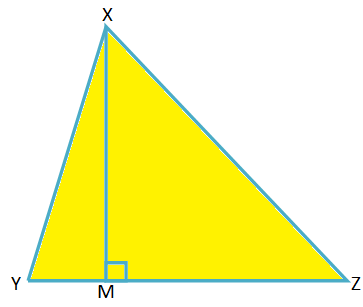
3. In ∆XYZ, ∠Z is acute and XM ⊥ YZ, M being the foot of the perpendicular. Prove that 2YZ ∙ ZM = YZ² + ZX² - XY².

Solution:

From the right-angled ∆XMY,

XY² = XM² + YM²

         = XM² + (YZ - ZM)²

         = XM² + YZ² + ZM² - 2YZ ∙ ZM (from algebra)

         = YZ² - 2YZ ∙ ZM + (XM² + ZM²)

         = YZ² - 2YZ ∙ ZM + XZ² (from right-angled ∆XMZ)

Therefore, 2YZ ∙ ZM = YZ² + ZX² – XY². (Proved)

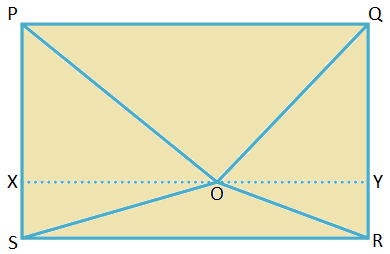
4. Let PQRS be a rectangle. O is a point inside the rectangle. Prove that OP² + OR² = OQ² + OS².

Solution:

PQRS is a rectangle for which PQ = SR = length and QR = PS = breadth.

Join OP, OQ, OR and OS.

Draw XY through O, parallel to PQ.

As ∠QPS and ∠RSP are right angles, ∆PXO, ∆SXO, ∆RYO and ∆QYO are right-angled triangles.

Therefore, by Pythagoras’ theorem,

OP² = PX² + OX²,

OR² = RY² + OY²,

OQ² = QY² + OY² and

OS² = SX² + OX²

Therefore, OP² + OR² = PX² + OX² + RY² + OY² ......... (i)

                OQ² + OS² = QY² + OY² + SX² + OX² ......... (ii)

But in the rectangle XSRY, SX = RY = breadth

and in the rectangle PXYQ, PX = QY = breadth.

Therefore, from (i) and (ii), OP² + OR² = OQ² + OS².

9th Grade Math

From Riders Based on Pythagoras’ Theorem to HOME PAGE