Rectangular Cartesian Coordinates of a Point

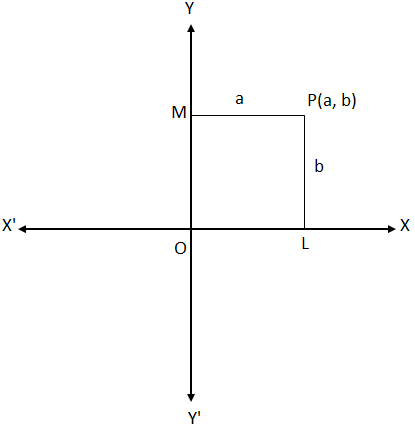
Take two intersecting lines XOX’ and YOY” in a plane which cut at O and are perpendicular to each other. Let P be a point in the plane. Draw perpendiculars from P to the line XoX’ and YoY’. 

Let them be PL and PM. Measure PL and PM in the same scale in mm, cm or m, etc. Let the measures of PL and PM be b units and a units respectively. Then (a, b) are called rectangular Cartesian coordinates of a point P.

The lines XOX’ and YOY’, called coordinate axes, together from the frame of reference in the Cartesian x-y plane for which

(i) XOX’ in called the x-axis,

(ii) YOY’ is called the y-axis, and

(iii) O is called the origin.

If (a, b) are the coordinates of the point P then a is called the x-coordinate or abscissa and b is called the y-coordinate or ordinate of a point P.

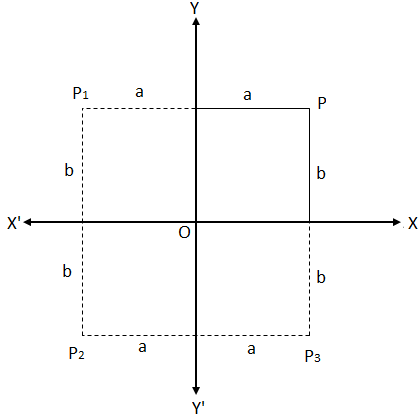
In the discussion above, we have seen that to determine the coordinates of the point P, we need to measure the lengths of PM and PL. We have found that the measures are a units and b units respectively.

But with the same measures of distances, the point P can be found in any of the three other positions in the same plane as shown in the adjoining diagram.

To determine the exact position of a point in a plane, we need to undedrstand the convention for signs of coordinates.

9th Grade Math

From Rectangular Cartesian Coordinates of a Point to HOME PAGE