Problems on Two Tangents to a Circle from an External Point

We will solve some Problems on two tangents to a circle from an external point.

1. If OX any OY are radii and PX and PY are tangents to the circle, assign a special name to the quadrilateral OXPY and justify your answer.

Solution:

OX = OY, are radii of a circle are equal.

PX = PY, as tangents to a circle from an external point are equal.

Therefore, OXPY is a kite.

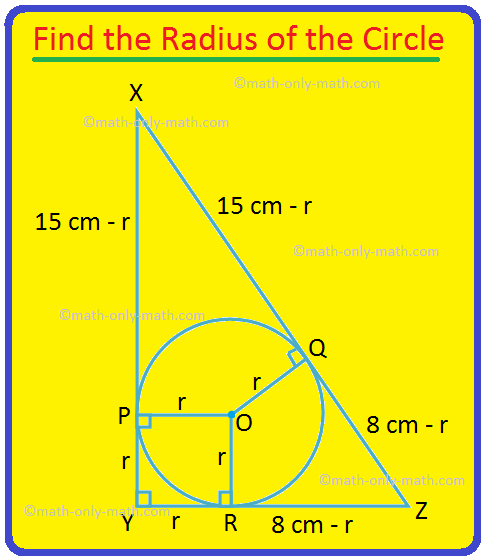
2. ∆XYZ is right angled at Y. A circle with centre O has been inscribed in the triangle. If XY = 15 cm and YZ = 8 cm, find the radius of the circle.

Solution:

Using Pythagoras’ theorem, we get

XZ = \(\sqrt{XY^{2} + YZ^{2}}\) = \(\sqrt{225 + 64 }\) cm = \(\sqrt{289}\) cm = 17 cm.

We draw OP ⊥ XY, OQ ⊥ YZ and OR ⊥ XZ.

Therefore, OP = OQ = OR = r, where r is the radius of the circle.

PYQO is a square.

Therefore, PY = YQ = r.

Therefore, XP = 15 cm – r and QZ = 8 cm – r.

Now, tangents drawn to a circle from an external point are equal.

Therefore, XR = XP = 15 cm – r and RZ = QZ = 8 cm – r.

But XR + RZ = XZ

⟹ 15 cm – r + 8 cm – r = 17 cm

⟹ 23 cm – 2r = 17 cm

⟹ 2r = 23 cm – 17 cm

⟹ 2r = 6 cm

⟹ r = 3 cm.

10th Grade Math

From Problems on Two Tangents to a Circle from an External Point to HOME PAGE

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit