Problems on Cumulative-Frequency Curve

We will discuss here some of the problems on frequency polygon.

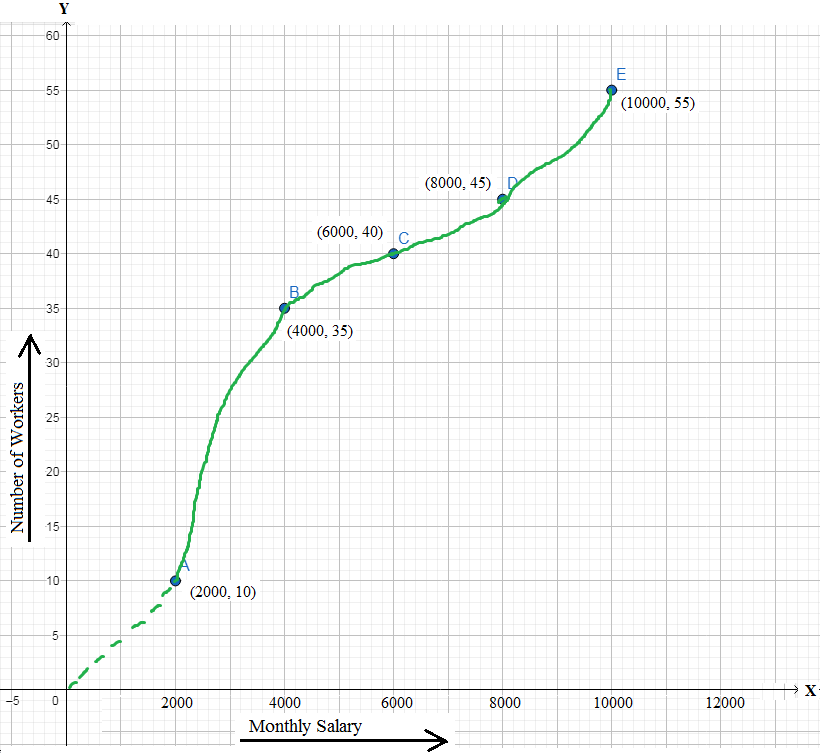
1. The monthly salaries of 55 workers of a factory are displayed in the following ogive.

Answer the following.

(i) How many workers have a monthly salary under $ 4000?

(ii) How many workers have a monthly salary more than or equal to $ 8000 but less than $ 10000?

(iii) Construct the frequency distribution table of the salaries of 55 workers.

Solution:

(i) 35. {Since the point on the ogive has the coordinates (4000, 35) corresponding to the point representing 4000 on the monthly salary axis.}

(ii) 10 (i.e., 55 – 45). {Since, according to the ogive, 55 workers have a salary less than $ 10000 and 45 workers have a salary less than $ 8000.}

(iii)

Therefore, the frequency distribution table of the salaries of 55 workers will be as below.

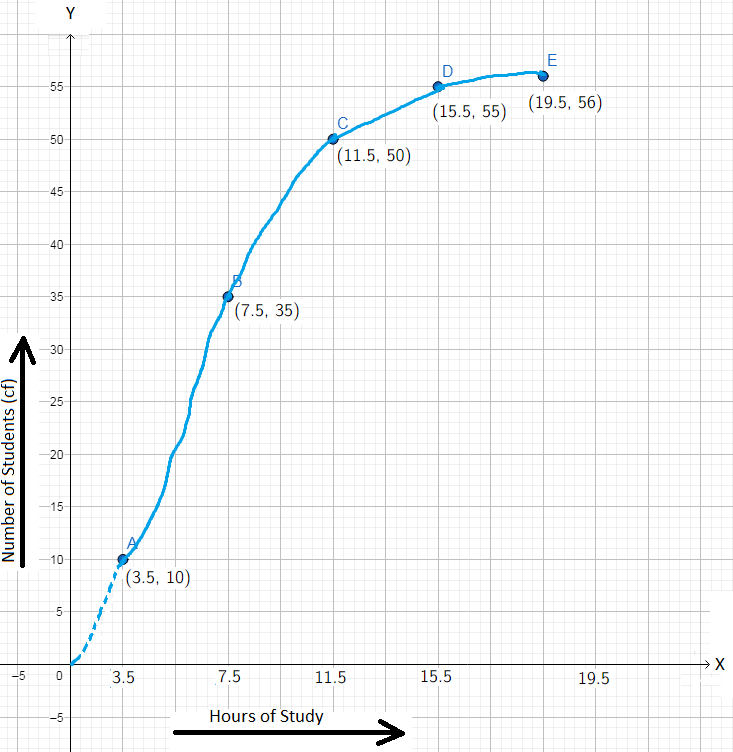
2. Construct an ogive for the following distribution.

Solution:

Here, the distribution is not continuous. Changing the intervals to overlapping intervals, we get the following cumulative-frequency table.

Taking the upper limit of an interval and its corresponding cumulative frequency as x- and y-coordinates respectively, plot the points (3.5, 10)), (7.5, 35), (11.5, 50), (15.5, 55) and (19.5, 56).

Scale: On the x-axis, 1 cm = 4 hours.

          On the y-axis, 1 mm = 1 student

10th Grade Math

From Problems on Cumulative -Frequency Curve