Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Plotting a Point in Cartesian plane
If the coordinates (x, y) of a point are given, one can plot in the Cartesian x-y plane by taking the following steps.
Step I: Observe the signs of the coordinates and determine the quadrant in which the point should be plotted.
Step II: Take a rectangular Cartesian frame of axes XOX’ and YOY’ cutting each other at right angles at O.
Step III: Take a point M on the x-axis on the side of the concerned quadrant such that the distance of the point M from the origin O equals the numerical value of the x-coordinate. Draw a perpendicular MN on the x-axis. Take a point P on this perpendicular such that MP is equal to the numerical value of the y-coordinate and P is in the concerned quadrant. Thus P is plotted according to its given coordinates.
Examples on plotting a point in Cartesian plane:
Plot the following points in Cartesian plane:
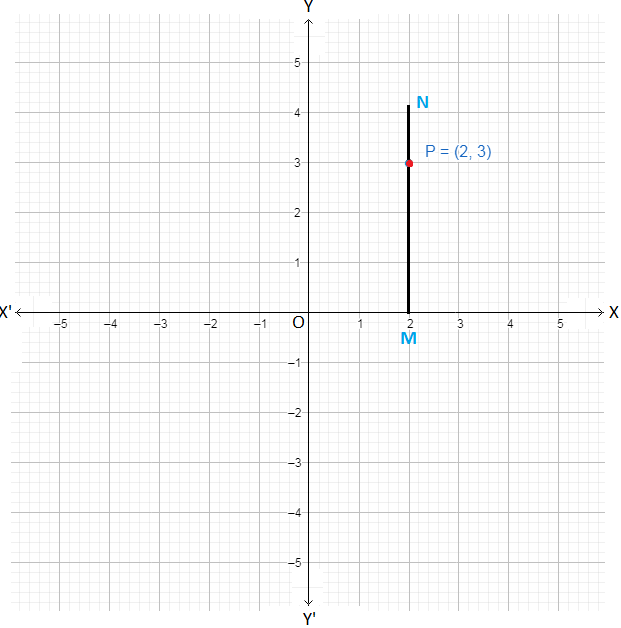
(i) (2, 3)
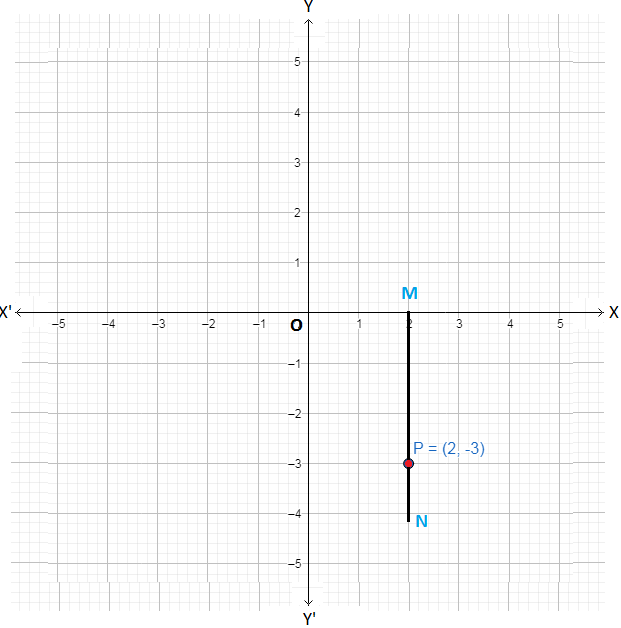
(ii) (2, -3)
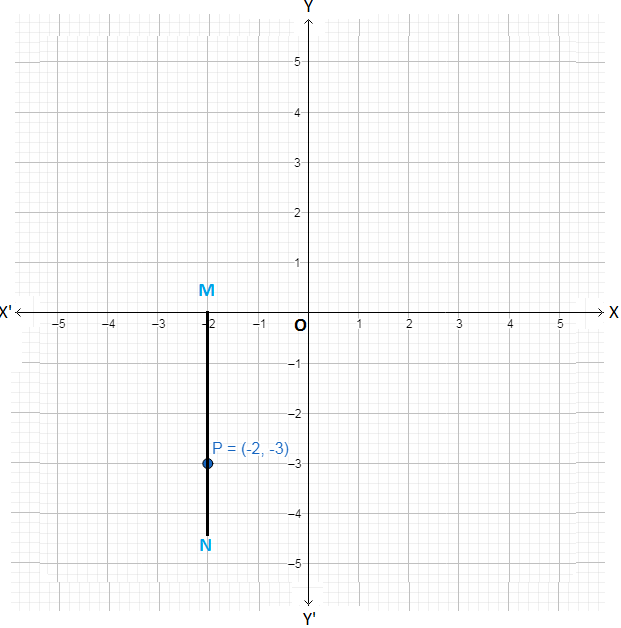
(iii) (-2, -3)
(iv) (-2, 3)
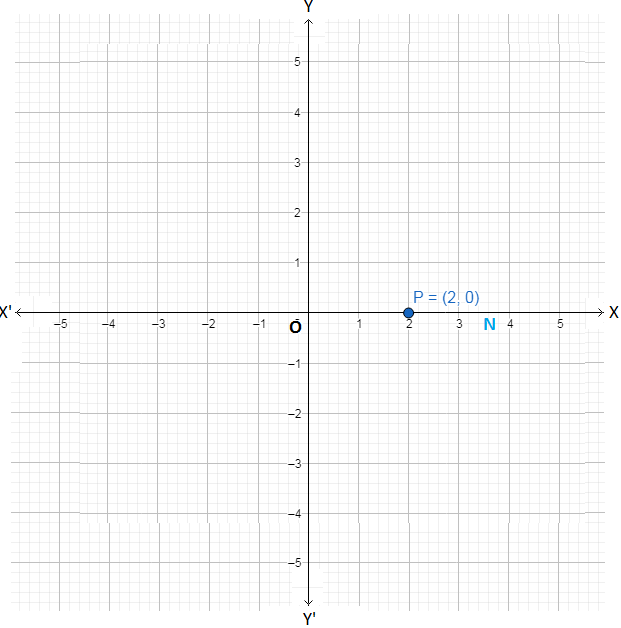
(v) (2, 0)
(vi) (0, -3)
Solution:
(i) (2, 3) is a point in the first quadrant because 2 > 0, 3 > 0. Following the steps 2 and 3 we plot the point P with co-ordinates (2, 3) as shown below.
(ii) (2, -3) is a point in the fourth quadrant because 2 > 0, -3 < 0. Following the steps 2 and 3 we plot the point P with co-ordinates (2, -3) as shown below.
(iii) (-2, -3) is a point in the third quadrant because -2 < 0, -3 < 0. Following the steps 2 and 3 we plot the point P with co-ordinates (-2, -3) as shown below.
(iv) (-2, 3) is a point in the second quadrant because -2 < 0, 3 > 0. Following the steps 2 and 3 we plot the point P with co-ordinates (-2, 3) as shown below.
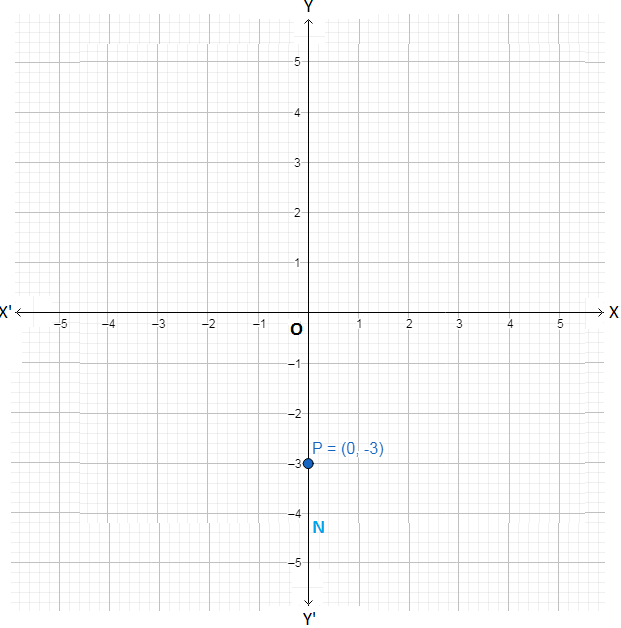
(v) (0, -3) is a point on the negative y-axis because x-coordinate = 0 and y-coordinate < 0. Following the steps 2 and 3 we plot the point P with co-ordinates (0, -3) as shown below.
These examples will help us to plot different co-ordinate points on Cartesian plane.
From Plotting a Point in Cartesian Plane to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.