Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Perimeter and Area of a Triangle
Here we will discuss about the perimeter and area of a triangle and some of its geometrical properties.
Perimeter, Area and Altitude of a Triangle:
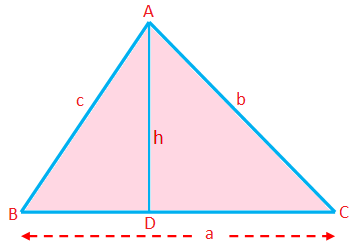
Perimeter of a triangle (P) = Sum of the sides = a + b + c
Semiperimeter of a triangle (s) = \(\frac{1}{2}\)(a + b + c)
Area of a triangle (A) = \(\frac{1}{2}\) × base × altitude = \(\frac{1}{2}\)ah
Here any side can be taken as base; the length of the perpendicular from the corresponding vertex to this side is the altitude.
Area = \(\sqrt{\textrm{s(s - a)(s - b)(s - c)}}\) (Heron’s formula)
Altitude (h) = \(\frac{\textrm{area}}{\frac{1}{2} \times \textrm{base}}\) = \(\frac{2\triangle}{a}\)
Solved Example on Finding the Perimeter, Semiperimeter and Area
of a Triangle:
The sides of a triangle are 4 cm, 5 cm and 7 cm. Find its perimeter, semiperimeter and area.
Solution:
Perimeter of a triangle (P) = Sum of the sides
= a + b + c
= 4 cm + 5 cm + 7 cm
= (4 + 5 + 7) cm
= 16 cm
Semiperimeter of a triangle (s) = \(\frac{1}{2}\)(a + b + c)
= \(\frac{1}{2}\)(4 cm + 5 cm + 7 cm)
= \(\frac{1}{2}\)(4 + 5 + 7) cm
= \(\frac{1}{2}\) × 16 cm
= 8 cm
Area of a triangle = \(\sqrt{\textrm{s(s - a)(s - b)(s - c)}}\)
= \(\sqrt{\textrm{8(8 - 4)(8 - 5)(8 - 7)}}\) cm\(^{2}\)
= \(\sqrt{\textrm{8 × 4 × 3 × 1}}\) cm\(^{2}\)
= \(\sqrt{96}\) cm\(^{2}\)
= \(\sqrt{16 × 6}\) cm\(^{2}\)
= 4\(\sqrt{6}\) cm\(^{2}\)
= 4 × 2.45 cm\(^{2}\)
= 9.8 cm\(^{2}\)
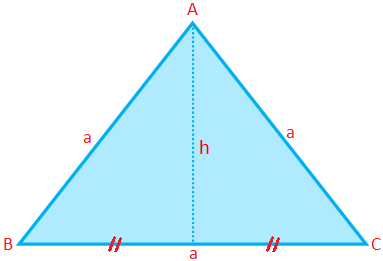
Perimeter, Area and Altitude of an Equilateral Triangle:
Perimeter of an equilateral triangle (P) = 3 × side = 3a
Area of an equilateral triangle (A) = \(\frac{√3}{4}\) × (side)\(^{2}\) = \(\frac{√3}{4}\) a\(^{2}\)
Altitude of an equilateral triangle (h) = \(\frac{√3}{4}\) a
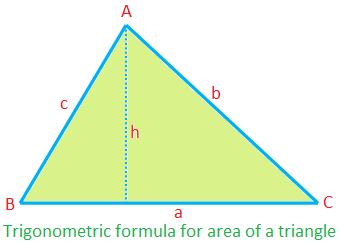
Trigonometric formula for area of a triangle:
Area of ∆ABC = \(\frac{1}{2}\) × ca sin B
= \(\frac{1}{2}\) × ab sin C
= \(\frac{1}{2}\) × bc sin A
(since, ∆ = \(\frac{1}{2}\) ah = \(\frac{1}{2}\) ca ∙ \(\frac{h}{c}\) = \(\frac{1}{2}\) ca sin B, etc.)
Solved Example on Finding the Area of a Triangle:
In a ∆ABC, BC = 6 cm, AB = 4 cm and ∠ABC = 60°. Find its area.
Solution:
Area of ∆ABC = \(\frac{1}{2}\) ac sin B = \(\frac{1}{2}\) × 6 × 4 sin 60° cm\(^{2}\)
= \(\frac{1}{2}\) × 6 × 4 × \(\frac{√3}{2}\) cm\(^{2}\)
= 6√3 cm\(^{2}\)
= 6 × 1.73 cm\(^{2}\)
= 10.38 cm\(^{2}\)
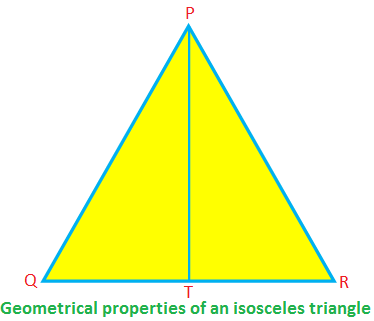
Some geometrical properties of an isosceles triangle:
In the isosceles ∆PQR, PQ = PR, QR is the base, and PT is the altitude.
Then, ∠PTR = 90°, QT = TR, PT\(^{2}\) + TR\(^{2}\) = PR\(^{2}\) (by Pythagoras’ theorem)
∠PQR = ∠PRQ, ∠QPT = ∠RPT.
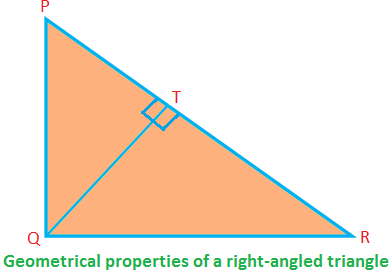
Some geometrical properties of a right-angled triangle:
In the right-angled ∆PQR, ∠PQR = 90°; PQ, QR are the sides (forming the right angle) and PR is the hypotenuse.
Then, PQ ⊥ QR (therefore, if QR is the base, PQ is the altitude).
PQ\(^{2}\) + QR\(^{2}\) = PR\(^{2}\) (by Pythagoras’ theorem)
Area of the ∆PQR = \(\frac{1}{2}\) ∙ PQ ∙ QR
⟹ PQ ∙ QR = 2 × area of the ∆PQR.
Again, area of the ∆PQR = \(\frac{1}{2}\) ∙ QT ∙ PR
⟹ QT ∙ PR = 2 × area of the ∆PQR.
Therefore, PQ ∙ QR = QT ∙ PR = 2 × Area of the ∆PQR.
Solved Examples on Perimeter and Area of a Triangle:
1. Find the perimeter of an equilateral triangle whose area is equal to that of a triangle with sides 21 cm, 16 cm and 13 cm.
Solution:
Let a side of the equilateral triangle = x.
Then, its area = \(\frac{√3}{4}\) x\(^{2}\)
Now, the area of the other triangle = \(\sqrt{\textrm{s(s - a)(s - b)(s - c)}}\)
Here, s = \(\frac{1}{2}\) (a + b + c)
= \(\frac{1}{2}\) (21 + 16 + 13) cm
= \(\frac{1}{2}\) 50 cm
= 25 cm
Therefore, area of the other triangle = \(\sqrt{\textrm{25(25 - 21)(25 - 16)(25 - 13)}}\) cm\(^{2}\)
= \(\sqrt{\textrm{25 ∙ 4 ∙ 9 ∙ 12}}\) cm\(^{2}\)
= 60\(\sqrt{\textrm{3}}\) cm\(^{2}\)
According to the question, \(\frac{√3}{4}\) x\(^{2}\) = 60\(\sqrt{\textrm{3}}\) cm\(^{2}\)
⟹ x\(^{2}\) = 240 cm\(^{2}\)
Therefore, x = 4√15 cm
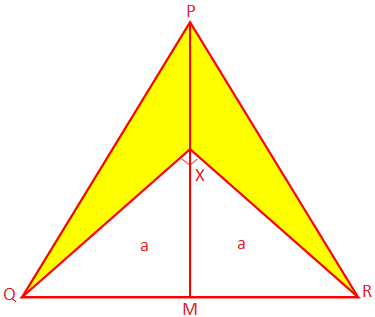
2. PQR is an isosceles triangle whose equal sides PQ and PR are 10 cm each, and the base QR measures 8 cm. PM is the perpendicular from P to QR and X is a point on PM such that ∠QXR = 90°. Find the area of the shaded portion.
Solution:
Since PQR is an isosceles triangle and PM ⊥ QR, QR is bisected at M.
Therefore, QM = MR = \(\frac{1}{2}\) QR = \(\frac{1}{2}\) × 8 cm = 4 cm
Now, PQ\(^{2}\) = PM\(^{2}\) + QM\(^{2}\) (by Pythagoras’ theorem)
Therefore, 10\(^{2}\) cm\(^{2}\) = PM\(^{2}\) + 4\(^{2}\) cm\(^{2}\)
or, PM\(^{2}\) = 10\(^{2}\) cm\(^{2}\) - 4\(^{2}\) cm\(^{2}\)
= 100 cm\(^{2}\) - 16 cm\(^{2}\)
= (100 - 16) cm\(^{2}\)
= 84 cm\(^{2}\)
Therefore, PM\(^{2}\) = 2√21 cm
Therefore, area of the ∆PQR = \(\frac{1}{2}\) × base × altitude
= \(\frac{1}{2}\) × QR × PM
= (\(\frac{1}{2}\) × 8 × 2√21) cm\(^{2}\)
= 8√21) cm\(^{2}\)
From geometry, ∆XMQ ≅ ∆XMR (SAS criterion)
We get, XQ =XR = a (say)
Therefore, from the right-angled ∆QXR, a\(^{2}\) + a\(^{2}\) = QR\(^{2}\)
or, 2a\(^{2}\) = 8\(^{2}\) cm\(^{2}\)
or, 2a\(^{2}\) = 64 cm\(^{2}\)
or, a\(^{2}\) = 32 cm\(^{2}\)
Therefore, a = 4√2 cm
Again, area of the ∆XQR = \(\frac{1}{2}\) × XQ × XR
= \(\frac{1}{2}\) × a × a
= \(\frac{1}{2}\) × 4√2 cm × 4√2 cm
= \(\frac{1}{2}\) × (4√2)\(^{2}\) cm\(^{2}\)
= \(\frac{1}{2}\) × 32 cm\(^{2}\)
= 16 cm\(^{2}\)
Therefore, area of the shaded portion = area of the ∆PQR - area of the ∆XQR
= (8√21) cm\(^{2}\) - 16 cm\(^{2}\)
= (8√21 - 16) cm\(^{2}\)
= 8(√21 - 2) cm\(^{2}\)
= 8 × 2.58 cm\(^{2}\)
= 20.64 cm\(^{2}\)
From Perimeter and Area of a Triangle to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
