Method of Constructing Frequency Polygon with the Help of Class Marks

We will discuss about the method of constructing a frequency polygon with the help of a class marks.

Step I: Prepare a frequency-distribution table overlapping intervals.

Step II: Find the class marks of the class intervals and locate them on the horizontal axis (class-interval axis). These will be the middle points of the line segments on the horizontal axis, representing the overlapping class intervals.

Step III: Draw perpendiculars to the horizontal axis at the points representing the class marks. The lengths of the perpendiculars should represent the frequencies of the corresponding class intervals. In other words, draw points which coordinates (a, b), where a = class mark and b = the corresponding frequency.

Step IV: Join the points plotted with coordinates (a, b), where a = class mark and b = the corresponding frequency.

Step V: Join the first plotted point to the point representing the class mark of the imaginary class interval before the first class interval of the distribution. Then, join the last plotted point to the point representing the class mark of the imaginary class interval after the last class interval. You can use dotted line segments for these.

Example: Draw a frequency polygon for the following distribution.

Solution:

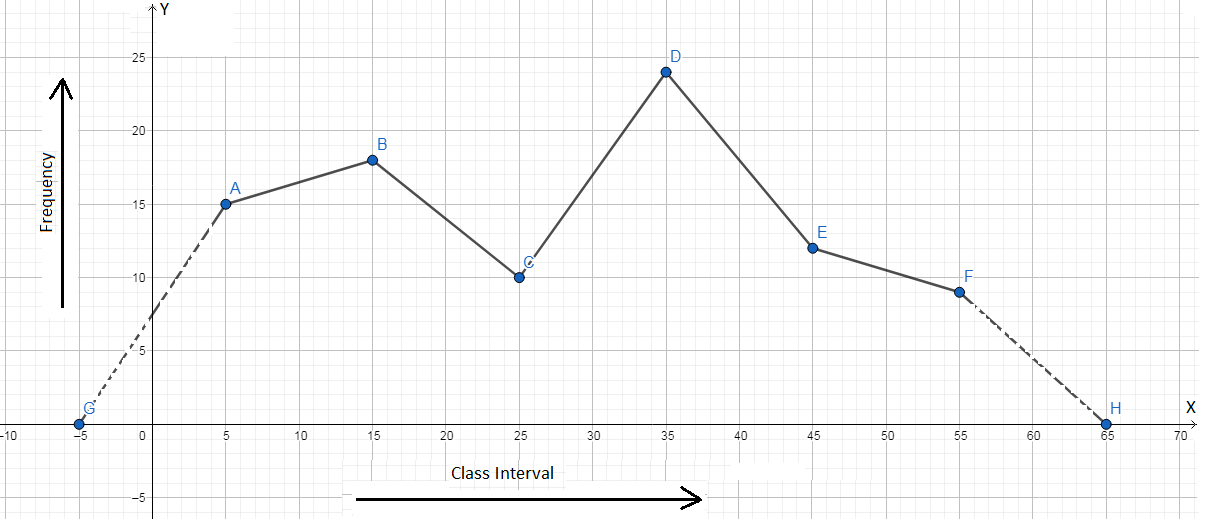
Here, the intervals are already overlapping (that is, the distribution is continuous). The class marks (i.e., midpoints of the intervals) of the class interval are 5, 15, 25, 35, 45 and 55 respectively.  So, using steps 2 and 3, plot the points (5, 15), (15, 18), 25, 10), (35, 24), (45, 12), (55, 9).

Following steps 4 and 5 after this, we get the frequency polygon as given below.

Scale: On the X-axis, 1 cm = width of one interval.

          On Y-axis, 1 cm = frequency 10.

10th Grade Math

From Method of Constructing a Frequency Polygon with the Help of a Class Marks to HOME PAGE