Subscribe to our YouTube channel for the latest videos, updates, and tips.
Finding the Mean from Graphical Representation
Here we will learn how to find the mean from graphical representation.
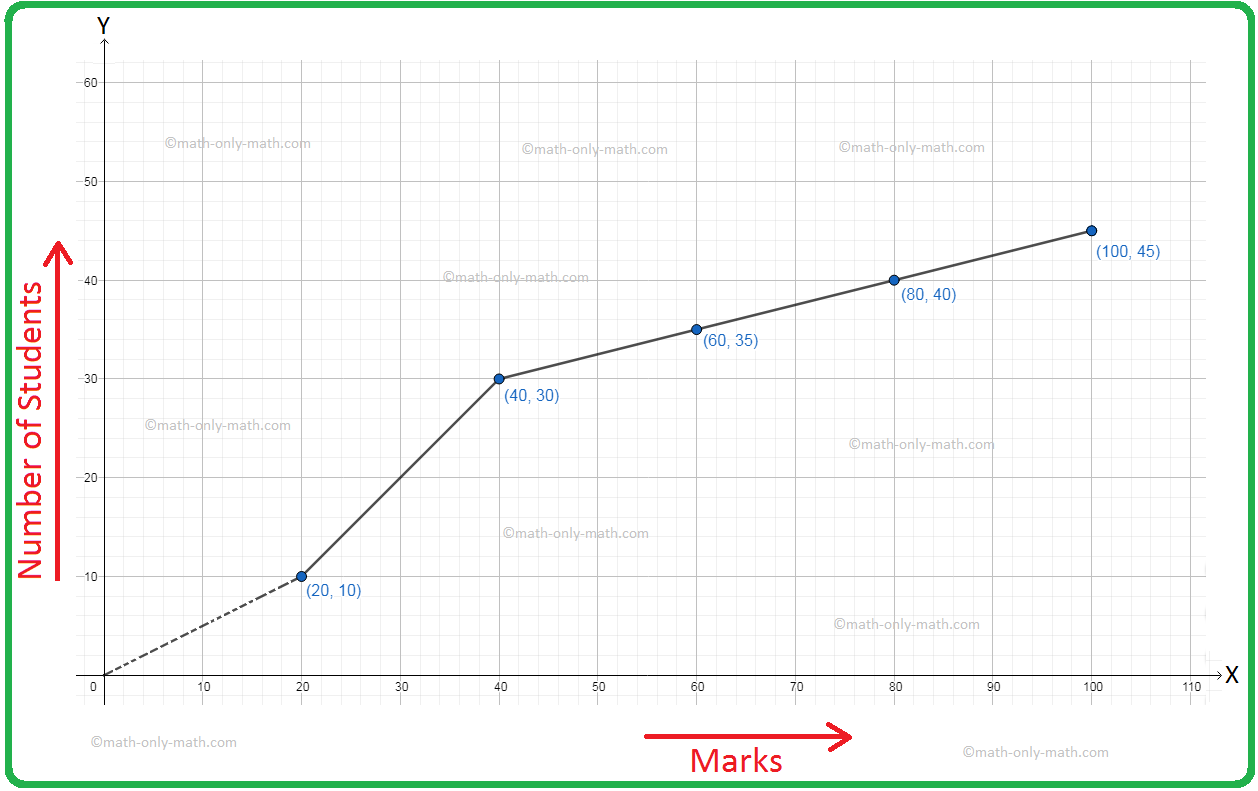
The ogive of the distribution of marks of 45 students is given below.
Find the mean of the distribution.
Solution:
The cumulative-frequency table is as given below.
Marks
Under 20
Under 40
Under 60
Under 80
Under 100
Number of Students
10
30
35
40
45
Writing in overlapping class intervals, the distribution is as below.
Marks
0 - 20
20 - 40
40 - 60
60 - 80
Under 100
Number of Students
10
20
5
5
5
The calculations are as given below.
|
Class Interval |
Class Mark (mi) |
Frequency (fi) |
mifi |
|
0 - 20 |
10 |
10 |
100 |
|
20 - 40 |
30 |
20 |
600 |
|
40 - 60 |
50 |
5 |
250 |
|
60 - 80 |
70 |
5 |
350 |
|
80 - 100 |
90 |
5 |
450 |
|
∑fi = 45 |
∑mifi = 1750 |
Therefore, mean A = ∑mifi∑fi
= 175045
= 38.89
From Finding the Mean from Graphical Representation to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
5th Grade Circle Worksheet | Free Worksheet with Answer |Practice Math
Jul 10, 25 11:41 AM
In 5th Grade Circle Worksheet you will get different types of questions on parts of a circle, relation between radius and diameter, interior of a circle, exterior of a circle and construction of circl… -
Construction of a Circle | Working Rules | Step-by-step Explanation |
Jul 09, 25 01:29 AM
Construction of a Circle when the length of its Radius is given. Working Rules | Step I: Open the compass such that its pointer be put on initial point (i.e. O) of ruler / scale and the pencil-end be… -
Combination of Addition and Subtraction | Mixed Addition & Subtraction
Jul 08, 25 02:32 PM
We will discuss here about the combination of addition and subtraction. The rules which can be used to solve the sums involving addition (+) and subtraction (-) together are: I: First add -
Addition & Subtraction Together |Combination of addition & subtraction
Jul 08, 25 02:23 PM
We will solve the different types of problems involving addition and subtraction together. To show the problem involving both addition and subtraction, we first group all the numbers with ‘+’ and… -
5th Grade Circle | Radius, Interior and Exterior of a Circle|Worksheet
Jul 08, 25 09:55 AM
A circle is the set of all those point in a plane whose distance from a fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.