Subscribe to our YouTube channel for the latest videos, updates, and tips.
Estimation in Operations on Numbers
To estimate sum and difference, we first round off each number to the nearest tens, hundreds, thousands or millions and then apply the required mathematical operation.
Solved example on Estimation in Operations on Numbers:
1. Find the actual and estimated sum of 126,289 and 375,484 by rounding off numbers to the nearest thousands.
Solution:
To round off to the nearest thousands place, we consider the number at ten-thousands place. Let us see the position of 126,289 on the number line.
We observe that 126,289 is closer to 100,000. Therefore, it is rounded down to 100,000. Next, we check the position of 375,484 on the number line.
We note that 375,484 is closer to 400,000. Therefore, it is rounded up to 400,000.
To find the estimated product or quotient, we round off numbers to the greatest place-value.
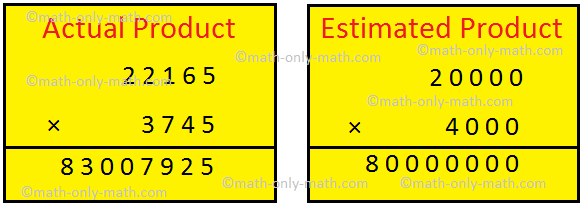
2. Find the actual and estimated product of 22,165 and 3,745 by rounding off numbers to the greatest place-value.
Solution:
22,165 is rounded off to the nearest ten-thousands. 3745 is rounded off to the nearest thousands.
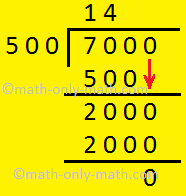
3. Estimate the quotient for 7,475 ÷ 510
Solution:
7,475 is rounded off to the nearest thousands
510 is rounded off to the nearest hundreds
7,475 is closer to 7,000
510 is closer to 500
So, 7,000 ÷ 500 = 14
Questions and Answers on Estimation in Operations on Numbers:
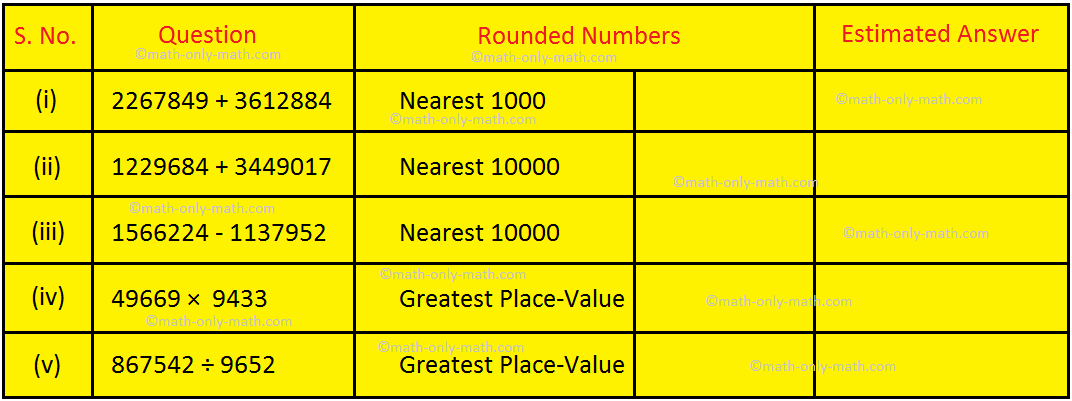
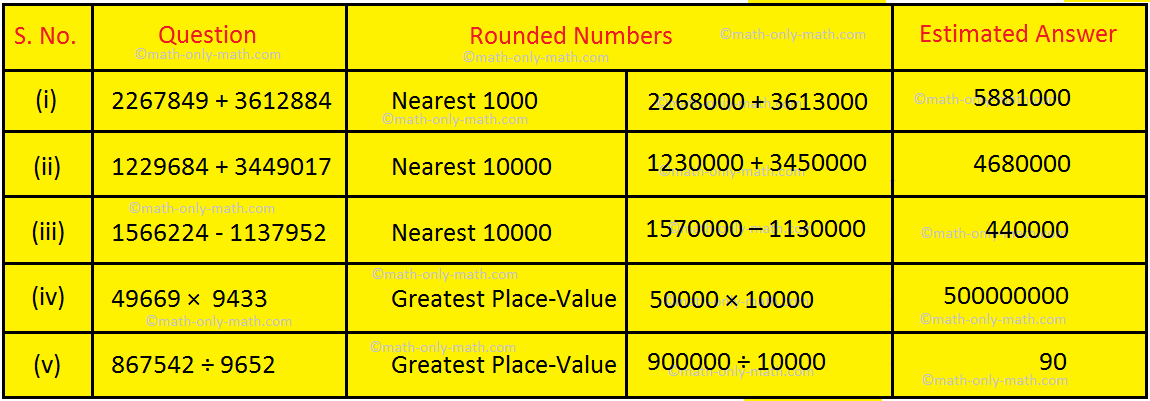
I. Estimate the given numbers and find the answer:
Answer:
II. Estimate and choose the right answer:
1. A shopkeeper has 93,450 packets to sketch pens. If each packet has 12 pens, then how many sketch pens are there in the shop.
(i) 900,000
(ii) 9,540,000
Answer: 900,000
2. Shelly has 6,782,344 mm of rope. She has another rope of length 2,539,886 mm. If both the ropes are attached, the estimated length nearest to 1000 will be
(i) 9,450,000
(ii) 9,322,000
Answer: 9,322,000
3. There are 1341 houses in a street. Each house uses 278 units of electricity energy. Estimated energy used by the houses nearest to 10 will be
(i) 375,200
(ii) 37,500
Answer: 375,200
5th Grade Math Problems
From Estimation in Operations on Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Average | Word Problem on Average | Questions on Average
May 17, 25 05:37 PM
In worksheet on average interest we will solve 10 different types of question. Find the average of first 10 prime numbers. The average height of a family of five is 150 cm. If the heights of 4 family -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed. -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 16, 25 11:13 AM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate -
Worksheet on Rounding Off Number | Rounding off Number | Nearest 10
May 15, 25 05:12 PM
In worksheet on rounding off number we will solve 10 different types of problems. 1. Round off to nearest 10 each of the following numbers: (a) 14 (b) 57 (c) 61 (d) 819 (e) 7729 2. Round off to
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.