Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Converse of Pythagoras’ Theorem
If in a triangle the sum of the squares of two sides is equal to the square of the third side then the triangle is a right-angled triangle, the angle between the first two sides being a right angle.
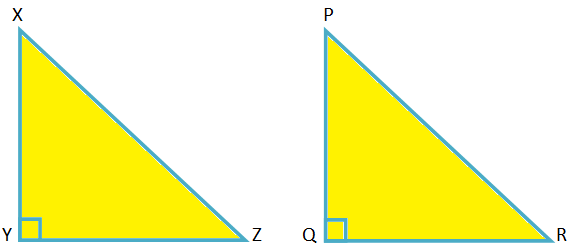
Given In the ∆XYZ, XY\(^{2}\) + YZ\(^{2}\) = XZ\(^{2}\)
To prove ∠XYZ = 90°
Construction: Draw a ∆PQR in which ∠PQR = 90° and PQ = XY, QR = YZ
Proof:
In the right-angled ∆PQR, PR\(^{2}\) = PQ\(^{2}\) + QR\(^{2}\)
Therefore, PR\(^{2}\) = XY\(^{2}\) + YZ\(^{2}\) = XZ\(^{2}\)
Therefore, PR = XZ
Now, in ∆XYZ and ∆PQR, XY = PQ, YZ = QR and XZ = PR
Therefore, ∆XYZ ≅ ∆PQR (by SSS criterion of congruency)
Therefore, ∠XYZ = ∠PQR = 90° (CPCTC)
Problems on Converse of Pythagoras’ Theorem
1. If the sides of a triangle are in the ratio 13:12:5, prove that the triangle is a right-angled triangle. Also state which angle is the right angle.
Solution:
Let the triangle be PQR.
Here the sides are PQ = 13k, QR = 12k and RP = 5k
Now, QR\(^{2}\) + RP\(^{2}\) = (12k)\(^{2}\) + (5k)\(^{2}\)
= 144k\(^{2}\) + 25k\(^{2}\)
= 169k\(^{2}\)
= (13k)\(^{2}\)
= PQ\(^{2}\)
Therefore, by converse of Pythagoras theorem, PQR is a right-angled triangle in which ∠R = 90°.
From Converse of Pythagoras’ Theorem to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.