Concept of Parallelogram

Here we will discuss about the concept of parallelogram.

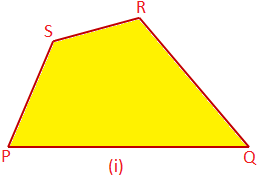
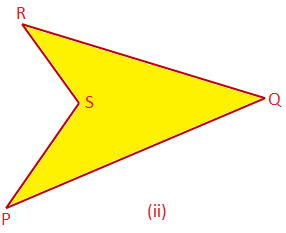
Quadrilateral: A rectilinear figure enclosed by four line segments is called a quadrilateral. In the adjoining figures, we have two quadrilaterals PQRS, each enclosed by four line segments PQ, QR, RS and SP which are called the sides of the quadrilateral.

The point of intersection of any two consecutive sides is called a vertex. 

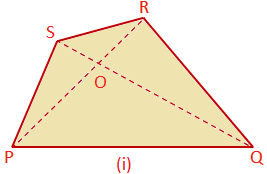
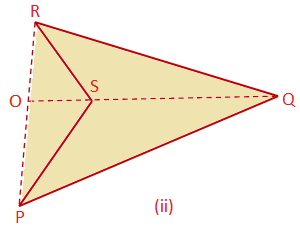
Here P, Q, R and S are the vertices. PR and QS are the two diagonals of the quadrilateral PQRS. In figure (i), the two diagonals cut each other internally at O. But in figure (ii), they cut each other externally at O when one of the diagonals is produced.

The quadrilateral in figure (i) is a convex quadrilateral, while in figure (ii), the quadrilateral is nonconvex. In a convex quadrilateral, each of the four angles, i.e., ∠QPS, ∠PQR, ∠QRS and ∠RSP as in figure (i), is less than 180°. But in a nonconvex quadrilateral, one of the four angles will be greater than 180°. In the above figure (ii), ∠PSR is greater than 180°.

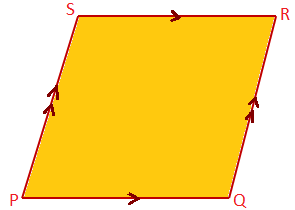
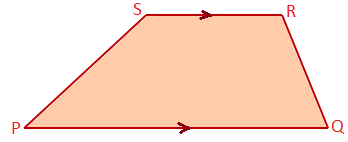
Parallelogram: A quadrilateral whose opposite sides are parallel, is called a parallelogram. In the given figure PQRS is a parallelogram in which PQ ∥ SR and PS ∥ QR.

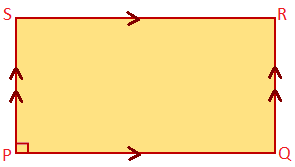
Rectangle: A parallelogram is called a rectangle if one of its angle is a right angle. In the given figure PQRS is a rectangle. Here PS ∥ QR, PQ ∥ SR and ∠P = 90°.

Consequently all angles will be right-angle.

Note: Every rectangle is a parallelogram but the converse is not true.

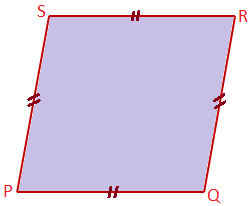
Rhombus: A quadrilateral whose all sides are equal, is called a rhombus. In the given figure, PQ = QR = RS = SP. So, PQRS is a rhombus.

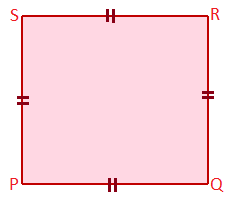
Square: A rhombus is called a square if its angles are right angle. In the given figure, PQ = QR = RS = SP and ∠SPQ = ∠PQR = ∠QRS = ∠RSP = 90°. So, PQRS is a square.

Trapezium: A quadrilateral whose one pair of opposite sides are parallel, is called a trapezium. In the given figure, PQRS  is a trapezium in which PQ ∥ SR and PS, QR are its oblique sides. 

If the oblique sides PS , QR are equal, the trapezium is called isosceles trapezium.

9th Grade Math

From Concept of Parallelogram to HOME PAGE