Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Area of a Polygon
In area of a polygon we will learn about polygon, regular polygon, central point of the polygon, radius of the inscribed circle of the polygon, radius of the circumscribed circle of a polygon and solved problems on area of a polygon.
Polygon: A figure bounded by four or more straight lines is called a polygon.
Regular Polygon: A polygon is said to be regular when all its sides are equal and all its angles are equal.
A polygon is named according to the number of sides it contains.
Given below are the names of some polygons and the number of sides contained by them.
Central Point of a Polygon:
The inscribed and the circumscribed circles of a polygon have the same centre, called the central point of the polygon.
Radius of the Inscribed Circle of a Polygon:
The length of perpendicular from the central point of a polygon upon any one of its sides, is the radius of the inscribed circle of the polygon.
The radius of the inscribed circle of a polygon is denoted by r.
Radius of the Circumscribed Circle of a Polygon:
The line segment joining the central point of a polygon to any vertex is the radius of the circumscribed circle of the polygon. The radius of the circumscribed circle of a polygon is denoted by R.
In the figure given below, ABCDEF is a polygon having central point O and one of its sides a unit. OL ⊥ AB.
Then, OL = r and OB = R
Area of a polygon of n sides
= n × (area ∆OAB) = n × ¹/₂ × AB × OL
= (ⁿ/₂ × a × r)
Now, A = \(\frac{1}{2}\) nar ⇔ a = \(\frac{2A}{nr}\) ⇔ na = \(\frac{2A}{r}\)
⇔ Perimeter = \(\frac{2A}{r}\)
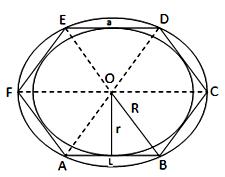
From right ∆OLB, we have:
OL² = OB² - LB² ⇔ r² = {R² - (ᵃ/₂)²}
⇔ r = √(R² - (a²/4)
Therefore, area of the polygon = {n/2 × a × √(R² - a²/4) square units.
In area of a polygon some of the particular cases such as;
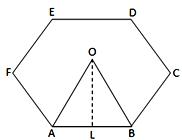
(i) Hexagon:
OL² = (OB² - LB²)
= {a² - (a/2)²} = (a² - a²/4) = 3a²/4
⇒ OL = {(√3)/2 × a}
⇒ Area ∆OAB = 1/2 × AB × OL
= {1/2 × a × (√3)/2 × a}
= (√3)a²/4
⇔ area of hexagon ABCDEF = {6 × (√3)a²/4} square units
= {3(√3)a²/2} square units.
Therefore, area of a hexagon = {3(√3)a²/2} square units.
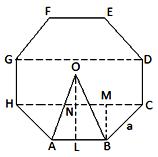
(ii) Octagon:
BM is the side of a square whose diagonal is BC = a.
Therefore, BM = \(\frac{a}{\sqrt{2}}\)
Now, OL = ON + LN
= ON + BM = (a/2 + a/√2)
⇔ Area of given octagon
= 8 × area of ∆OAB = 8 × 1/2 × AB × OL
= 4 × a × (a/2 + a/√2) = 2a² (1 + √2) square units.
Therefore, area of an octagon = 2a² (1 + √2) square units.
We will solve the examples on different names of the area of a polygon.
Area of a Polygon
1. Find the area of a regular hexagon each of whose sides measures 6 cm.
Solution:
Side of the given hexagon = 6 cm.
Area of the hexagon = {3√(3)a²/2} cm²
= (3 × 1.732 × 6 × 6)/2 cm²
= 93.528 cm².
2. Find the area of a regular octagon each of whose sides measures 5 cm.
Solution:
Side of the given octagon = 5 cm.
Area of the octagon = [2a² (1 + √2) square units
= [2 × 5 × 5 × (1 + 1.414)] cm²
= (50 × 2.414) cm²
= 120.7 cm².
3. Find the area of a regular pentagon each of whose sides measures 5 cm and the radius of the inscribed circle is 3.5 cm.
Solution:
Here a = 5 cm, r = 3.5 cm and n = 5.
Area of the pentagon = (n/2 × a × r) square units
= (5/2 × 5 × 7/2) cm²
= 43.75 cm².
4. Each side of a regular pentagon measures 8 cm and the radius of its circumscribed circle is 7 cm. Find the area of the pentagon.
Solution:
Area of the pentagon = {n/2 × a × √(R² - a²/4) square units
= {5/2 × 8 × √(7² - 64/4)} cm²
= {20 × √(49 - 16)} cm²
= (20 × √33) cm²
= (20 × 5.74) cm²
= (114.8) cm².
● Area of a Trapezium
● Area of a Trapezium - Worksheet
Worksheet on Area of a Polygon
8th Grade Math Practice
From Area of a Polygon to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
