Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Application Problems on Area of a Circle
We will discuss here about the Application problems on Area of a circle.
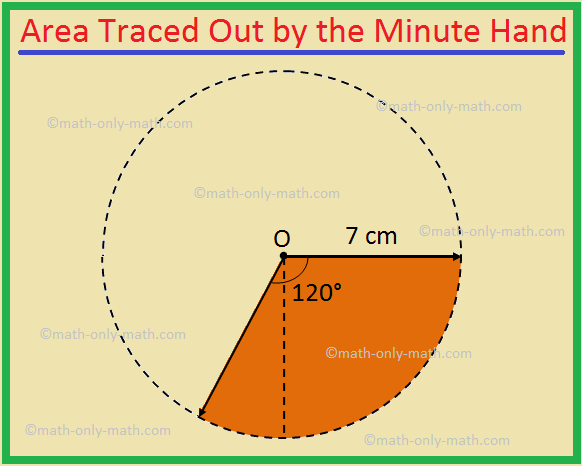
1. The minute hand of a clock is 7 cm long. Find the area traced out by the minute hand of the clock between 4.15 PM to 4.35 PM on a day.
Solution:
The angle through which the minute hand rotates in 20 minutes (i.e., 4:35 PM – 4:15 PM) is \(\frac{20}{60}\) × 360°, i.e., 120°
Therefore, the required area = The area of the sector of central angle 120°
= \(\frac{θ}{360}\) × πr2
= \(\frac{120}{360}\) × \(\frac{22}{7}\) × 72 cm2, [Since, θ = 120, r = 7 cm]
= \(\frac{1}{3}\) × 22 × 7 cm2.
= \(\frac{154}{3}\) cm2.
= 51\(\frac{1}{3}\) cm2.
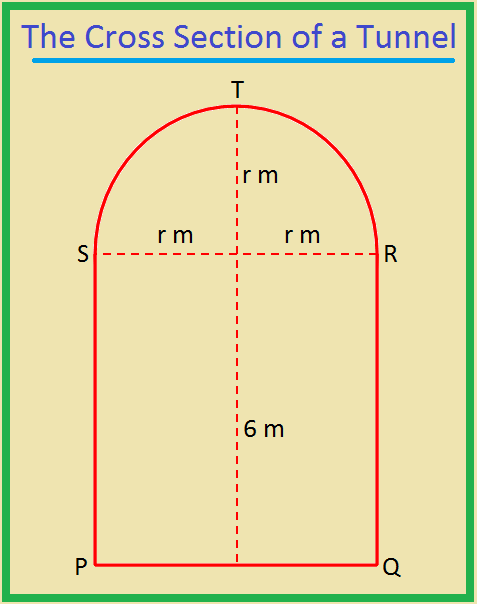
2. The cross section of a tunnel is in the shape of a semicircle surmounted on the longer side of a rectangle whose shorter side measures 6 m. If the perimeter of the cross section is 66 m, find the breadth and height of the tunnel.
Solution:
Let the radius of the secicircle be r m.
Then, the perimeter of the cross section
= PQ + QR +PS +
Semicircle STR
= (2r + 6 + 6 + πr) m
= (2r + 12 + \(\frac{22}{7}\) r) m
= (12 + 2r + \(\frac{22}{7}\) r) m
= (12 + \(\frac{36}{7}\) r) m
Therefore, 66m = (12 + \(\frac{36}{7}\) r) m
⟹ 66 = 12 + \(\frac{36}{7}\) r
⟹ 12 + \(\frac{36}{7}\) r = 66
⟹ \(\frac{36}{7}\) r = 66 - 12
⟹ \(\frac{36}{7}\) r = 54
⟹ r = 54 × \(\frac{7}{36}\)
⟹ r = \(\frac{21}{2}\).
Therefore, PQ = Breadth of the tunnel = 2r m = 2 × \(\frac{21}{2}\) = 21 m.
And height of the tunnel = r m + 6 m
= \(\frac{21}{2}\) m + 6 m
= \(\frac{21}{2}\) m + 6 m
= \(\frac{33}{2}\) m
= 16.5 m.
From Application Problems on Area of a Circle to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.