Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Null Matrix
If each element of an m × n matrix be 0, the null element of F, the matrix is said to be the null matrix or the zero matrix of order m × n and it is denoted by Om,n. It is also denoted by O, when no confusion regarding its order arises.
Null or zero Matrix: Whether A is a rectangular or square matrix, A - A is a matrix whose every element is zero. The matrix whose every element is zero is called a null or zero matrix and it is denoted by 0.
Thus for A and 0 of the same order we have A + 0 = A
For example,
[00] is a zero matrix of order 1 × 2.
[00] is a zero or null matrix of order 2 × 1.
[0000] is a null matrix of order 2 × 2.
[564109] is a null matrix of order 2 × 3.
Problems on Null or zero matrix:
1. Find two nonzero matrices whose product is a zero matrix.
Solution:
Let A = [1001] and B = [0001] be two non-zero matrices.
But AB = [1001] [0001] = [0000] is a null matrix.
2. If A = [12−1−1], show that A2 + I = 0.
(I and 0 being identity and null matrices of order 2).
Solution:
Given, A = [12−1−1]
Now A2 = [12−1−1][12−1−1] = [−100−1]
Therefore, A2 + I = [−100−1] + [1001] = [0000]
Thus, A2 + I = 0.
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Area, Perimeter and Volume | Square, Rectangle, Cube,Cubo
Jul 25, 25 12:21 PM
In this worksheet on area perimeter and volume you will get different types of questions on find the perimeter of a rectangle, find the perimeter of a square, find the area of a rectangle, find the ar… -
Worksheet on Volume of a Cube and Cuboid |The Volume of a RectangleBox
Jul 25, 25 03:15 AM
We will practice the questions given in the worksheet on volume of a cube and cuboid. We know the volume of an object is the amount of space occupied by the object.1. Fill in the blanks: -
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 24, 25 03:46 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
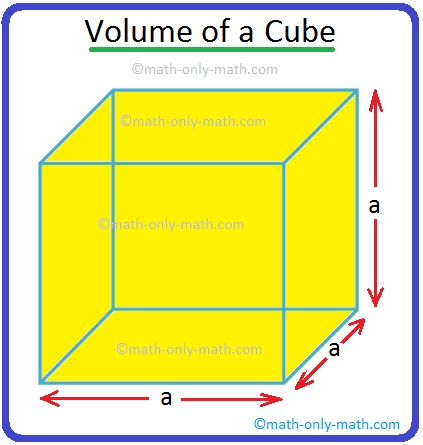
Volume of a Cube | How to Calculate the Volume of a Cube? | Examples
Jul 23, 25 11:37 AM
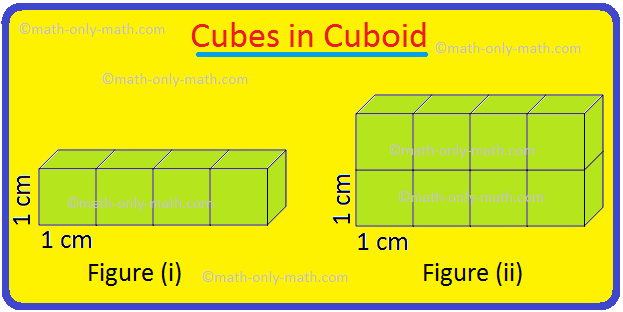
A cube is a solid box whose every surface is a square of same area. Take an empty box with open top in the shape of a cube whose each edge is 2 cm. Now fit cubes of edges 1 cm in it. From the figure i… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on…



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.