Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Direct Variation
When two variables change in proportion it is called as direct variation. In direct variation one variable is constant times of other. If one variable increases other will increase, if one decrease other will also decease. This means that the variables change in a same ratio which is called as constant of variation.
Direct variation is the simplest type of variation and in practical life we can find many situations which can be co-related with direct variation.
If two variables A and B are so related that when A increases ( or decreases ) in a given ratio, B also increases ( or, decreases ) in the same ratio, then A is said to vary directly as B ( or, A is said to vary as B ).
This is symbolically written as, A ∝ B (read as, ‘A varies as B’ ).
Suppose a train moving at a uniform speed travels d km. in t minutes. Now, consider the following table:
| d (km) | 24 | 12 | 48 | 36 |
| t (min) | 30 | 15 | 60 | 45 |
Like in a math examination if for one problem solving we can score 10 numbers, so five problems solving we can get 50 numbers. This can be explained with a direct variation equation. If T denotes total numbers scored, N denotes numbers of problem solved and K denotes numbers can be scored for solving a problem, then the direct variation equation for this situation will be T = KN.
As the numbers for a problem can be scored is fixed, it is a constant = K = TN = 10
For solving 5 problems total numbers scored T = KN = 10 x 5 = 50.
From the above example we can understand that the ratio of two variables is a constant K and T, N are the variables which changes in proportion with value of constant.
Direct variation can be by a linear equation Y = KX where K is a constant. When the value of constant is higher, the change of variable Y is significantly for small change of X. But when the value of K is very small, Y changes very less with change of X. For this case K is equivalent to the ratio of change of two variables. So σYσX = K when K is very small.
Now we will solve some problems on direct variation:
1. If P varies directly as Q and the value of P is 60 and Q is 40, what is the equation that describes this direct variation of P and Q?
Solution:
As P varies directly with Q, ratio of P and Q is constant for any value of P and Q.
So constant K = PQ = 6040 = 32
So the equation that describes the direct variation of P and Q is P = 32Q.
2. If a car runs at a constant speed and takes 3 hrs to run a distance of 180 km, what time it will take to run 100 km?
Solution:
If T is the time taken to cover the distance and S is the distance and V is the speed of the car, the direct variation equation is S= VT where V is constant.
For the case given in the problem,
180 = V × 3 or V = 1803 = 60
So speed of the car is 60kmph and it is constant.
For 100 km distance
S = VT or 100 = 60 × T
T = 10060 = 53 hrs = 1 hr 40 mins.
So it will take 1 hr 40 mins time.
3. In X is in direct variation with square of Y and when X is 4, Y is 3. What is the value of X when Y is 6?
Solution:
From the given problem direct variation equation can be expressed as
X = KY2
For the given case
4 = K × 32
or, 4 = 9K
or, K = 49
So when Y is 6,
X = 49 × 6 = 83
So the value of X is 83.
● Variation
- What is Variation?
- Direct Variation
- Inverse Variation
- Joint Variation
- Theorem of Joint Variation
- Worked out Examples on Variation
- Problems on Variation
From Direct Variation to Home Page
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Area, Perimeter and Volume | Square, Rectangle, Cube,Cubo
Jul 25, 25 12:21 PM
In this worksheet on area perimeter and volume you will get different types of questions on find the perimeter of a rectangle, find the perimeter of a square, find the area of a rectangle, find the ar… -
Worksheet on Volume of a Cube and Cuboid |The Volume of a RectangleBox
Jul 25, 25 03:15 AM
We will practice the questions given in the worksheet on volume of a cube and cuboid. We know the volume of an object is the amount of space occupied by the object.1. Fill in the blanks: -
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 24, 25 03:46 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
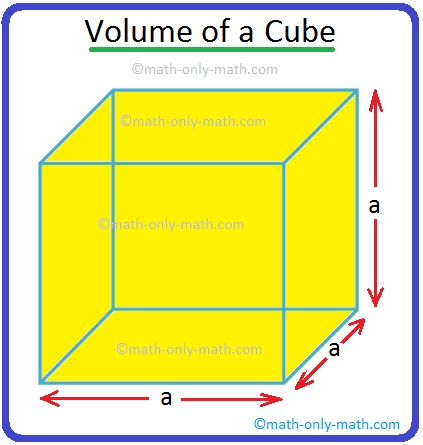
Volume of a Cube | How to Calculate the Volume of a Cube? | Examples
Jul 23, 25 11:37 AM
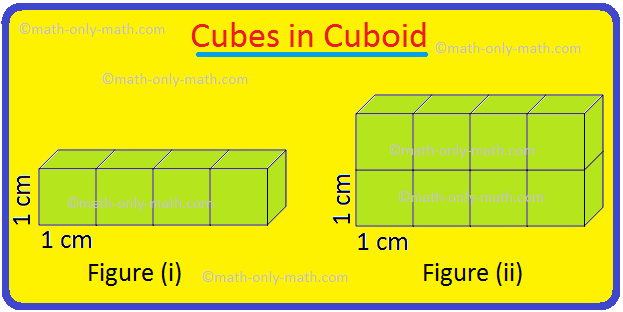
A cube is a solid box whose every surface is a square of same area. Take an empty box with open top in the shape of a cube whose each edge is 2 cm. Now fit cubes of edges 1 cm in it. From the figure i… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on…



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.