Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Decimal as Fraction
We will discuss how to express decimal as fraction.
0.5 = 510
0.05 = 5100
0.005 = 51000
2.5 = 2510
2.25 = 225100
2.275 = 22751000
To convert a decimal into a fraction, remember the following steps.
Step I: Write the number as the numerator omitting the decimal point.
Step II: Write 1 in the denominator and add zeroes to it equal to the number of decimal places.
Note: When a decimal is read, each digit of the decimal part is read separately.
Let us consider some of the following examples on expressing a decimal as a fraction.
1. Convert 2.12 into a fraction.
Solution:
|
2.12 = 2 + 1 tenth + 2 hundredths = 2 + 110 + 2100 = 2 + 1×1010×10 + 2100 = 2 + 10100 + 2100 = 2 + 10+2100 = 2 + 12100 = 2 + 325 = 2325 |
We write the place value of digits of decimal and then add as usual. |
2. Convert 5.125 into a fraction.
Solution:
|
5.125 = 5 + 1 tenth + 2 hundredths + 5 thousandths = 5 + 110 + 2100 + 51000 = 5 + 1×10010×100 + 2×10100×10 + 51000 = 5 + 1×10010×100 + 2×10100×10 + 51000 = 5 + 1001000 + 201000 + 51000 = 5 + 100+20+51000 = 5 + 1251000 = 5 + 18 = 518 |
We write the place value of digits of decimal and then add as usual. |
Express the following decimals in expanded form:
3.62 = 3 × 1 + 610 + 210
75.86 = 7 × 10 + 5 × 1 + 810 + 610
216.894 = 2 × 100 + 1 × 10 + 6 × 1 + 810 + 9100 + 41000
0.562 = 510 + 6100 + 21000
Express the following as decimal numbers:
For examples:
610 + 3100 = 0.63
610 + 3100 + 51000 = 0.635
4 × 1 + 310 + 2100 = 4.32
7 × 10 + 2 × 1 + 810 + 9100 = 72.89
Convert the following decimals to fractions in their lowest terms.
For examples:
0.36 = 36100 = 925 [36÷4100÷4 = 925]
5.65 = 5 + 0.65 = 5 + 65100 = 565100 = 51320]
14.05 = 14 + 0.05 = 14 + 5100 = 145100 = 14120]
3.004 = 3 + 0.004 = 3 + 41000 = 341000 = 31250]
Note: We always reduce the fraction converted from a decimal to its lowest form.
Questions and Answers on Conversion of a Decimals to a Fractions:
I. Convert the following decimals as fractions or mixed numerals:
(i) 0.6
(ii) 0.09
(iii) 3.65
(iv) 12.132
(v) 16.5
(vi) 5.46
(vii) 12.29
(viii) 0.008
(ix) 8.08
(x) 162.434
II. Express the following in the expanded form.
(i) 46.25
(ii) 115.32
(iii) 14.568
(iv) 19.005
(v) 77.777
III. Write as decimals:
(i) 2 × 1 + 710 + 4100
(ii) 3 × 10 + 5 × 1 + 810 + 31000
(iii) 7 × 100 + 4 × 10 + 5 × 1 + 41000
(iv) 9 × 100 + 710
(v) 5100 + 81000
From Decimal as Fraction to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
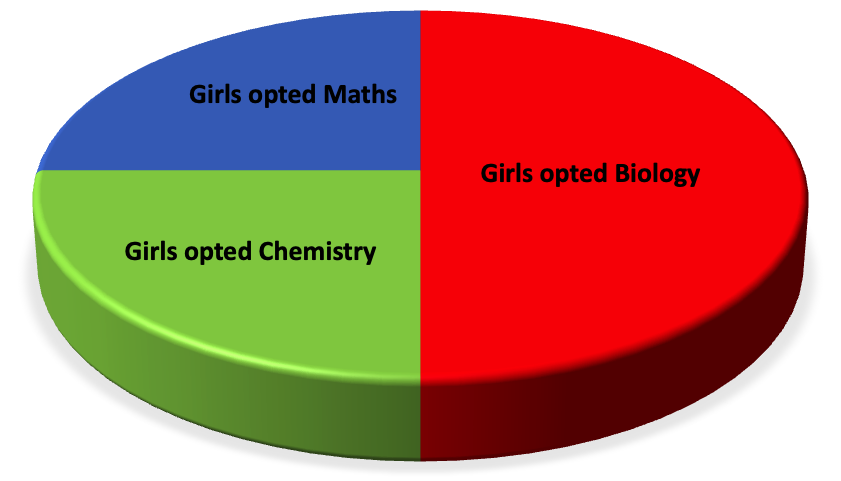
5th Grade Pie Chart | Definition of Pie Chart | Construction |Examples
Jul 31, 25 05:12 PM
Data can also be represented in a circle. This method, to represent data, is called a pie chart. Let us understand this method with the help of an example. -
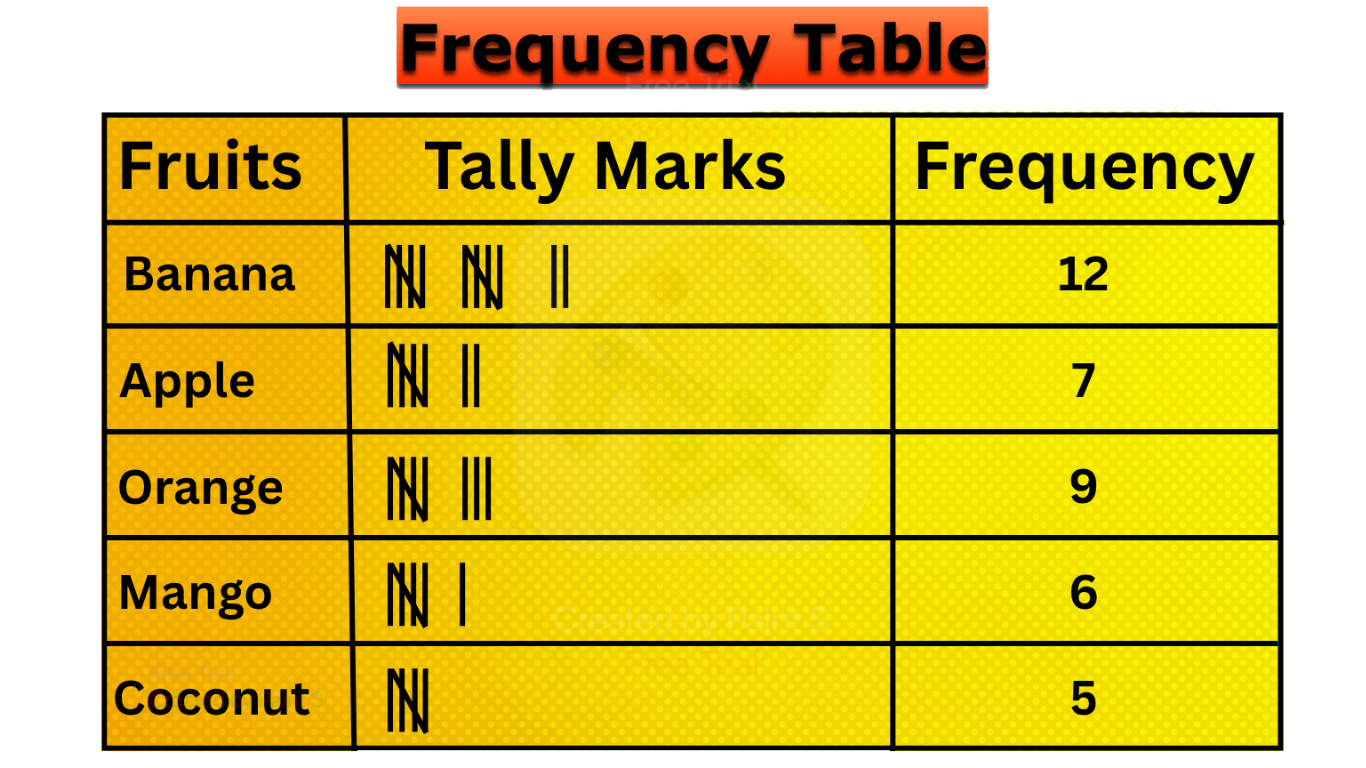
Frequency Distribution |Tally Marks |Frequency Distribution Table
Jul 31, 25 12:23 PM
What is frequency distribution?The number of times a particular observation occurs in a given data is called its frequency. In 7ᵗʰ grade and 8ᵗʰ grade frequency distribution, -
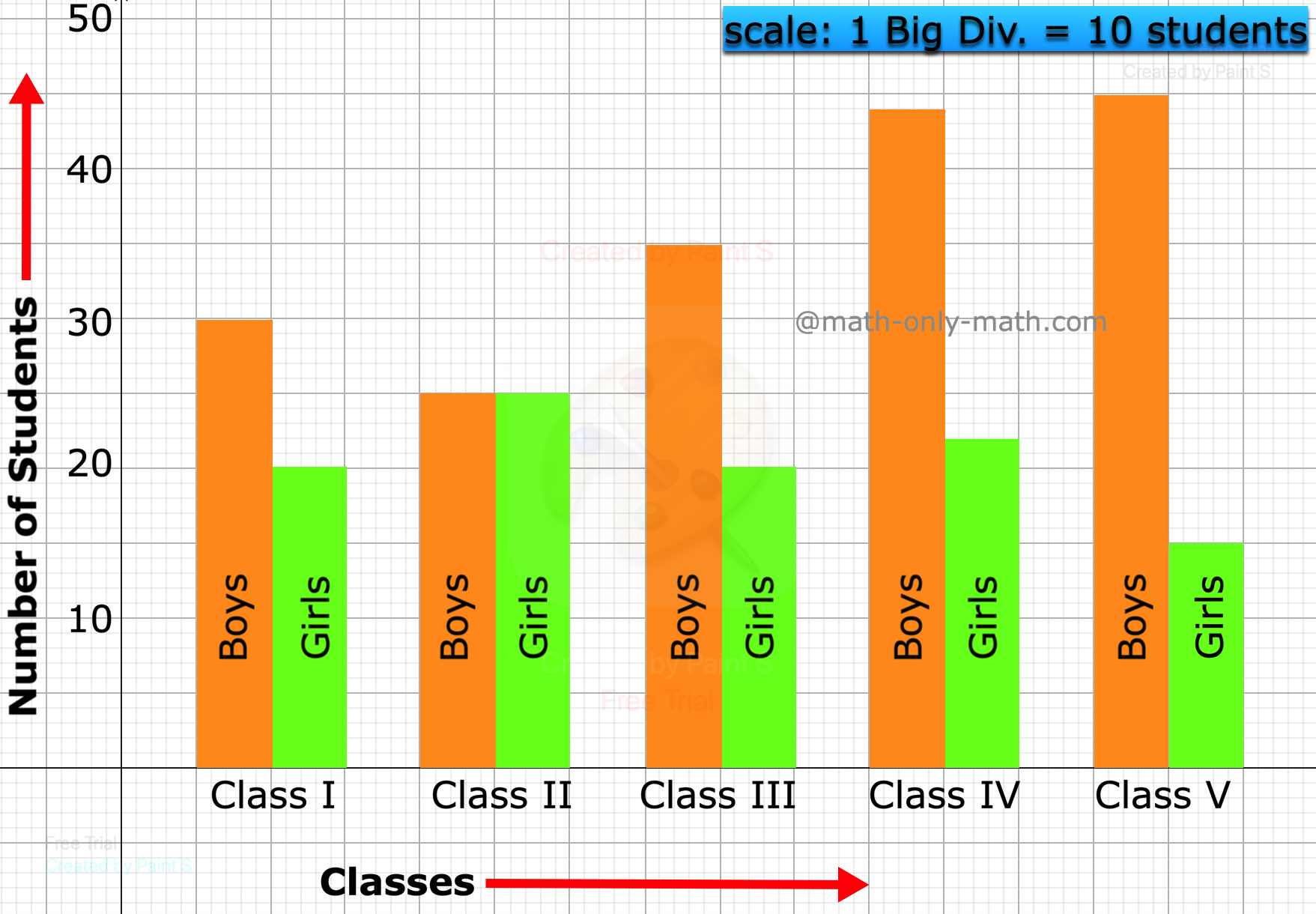
5th Grade Bar Graph | Definition | Interpret Bar Graphs|Free Worksheet
Jul 31, 25 05:16 AM
We learn how to represent the data on the bar graph. Data can be represented by bars (like rectangle) whose lengths represent numerical values. One can use horizontal or vertical bars. Instead of rect… -
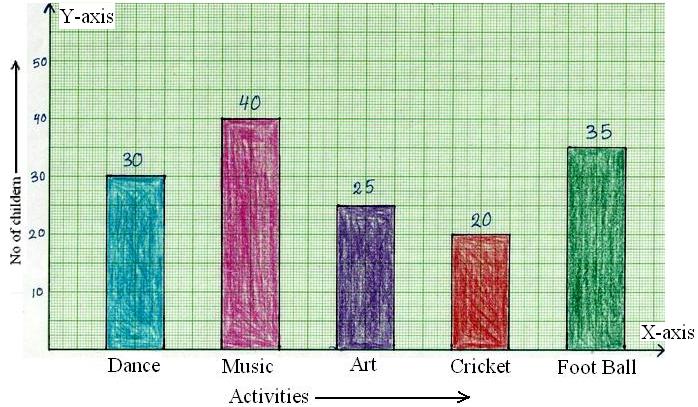
Construction of Bar Graphs | Examples on Construction of Column Graph
Jul 31, 25 03:35 AM
Now we will discuss about the construction of bar graphs or column graph. In brief let us recall about, what is bar graph? Bar graph is the simplest way to represent a data. In consists of rectangular… -
Successor and Predecessor | Successor of a Whole Number | Predecessor
Jul 29, 25 12:59 AM
The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number…


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.