Subscribe to our YouTube channel for the latest videos, updates, and tips.
Congruent Line-segments
In congruent line-segments we will learn how to recognize that two line-segments are congruent.
Two equal line-segments, lying in the same straight line and sharing a common vertex.
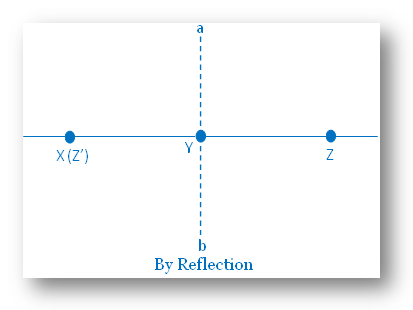
Here, two line-segments XY and YZ lying in the same straight line are equal. This is to be verified that they are congruent.
|
ab is perpendicular drawn at Y on XZ. With respect to ab, the image of ZY is YZ’. XY = YZ Hence, Z’ lies on X
Therefore, XY ≅ YZ |
|
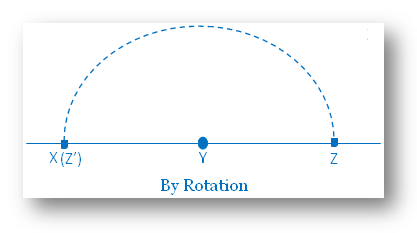
Taking Y as the centre of rotation and rotating YZ through an angle 180° in anticlockwise direction, the image YZ’ is obtained, where Z’ lies on X Therefore, XY ≅ YZ |
Two line segments lie on the same plane but at different positions.
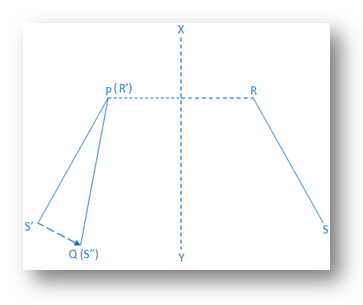
PQ and RS are two equal line segments on the same plane but on different positions. It is verified that they are congruent line-segments.
|
Perpendicular bisector XY of PR is drawn. Taking XY as the axis of reflection, the image of RS and PS’. Now taking P as the centre of rotation and rotating PS’ through such an angle (in anti-clock wise direction), so that PS’ coincides with PQ. Since PS’ that is RS = PQ. Hence S’ lies on Q and its new name is D”. |
Conditions for the Congruence of Triangles
Right Angle Hypotenuse Side congruence
Converse of Pythagorean Theorem
7th Grade Math Problems
8th Grade Math Practice
From Congruent Line-segments to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Average | Word Problem on Average | Questions on Average
May 19, 25 02:53 PM
In worksheet on average we will solve different types of questions on the concept of average, calculating the average of the given quantities and application of average in different problems. -
8 Times Table | Multiplication Table of 8 | Read Eight Times Table
May 18, 25 04:33 PM
In 8 times table we will memorize the multiplication table. Printable multiplication table is also available for the homeschoolers. 8 × 0 = 0 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed. -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 16, 25 11:13 AM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.