Volume and Surface Area of Cuboid
What is Cuboid?
A cuboid is a solid with six rectangular plane faces, for example, a brick or a matchbox. Each of these is made up of six plane faces which are rectangular. Remember that since a square is a special case of a rectangle, a cuboid may have square faces too.
The
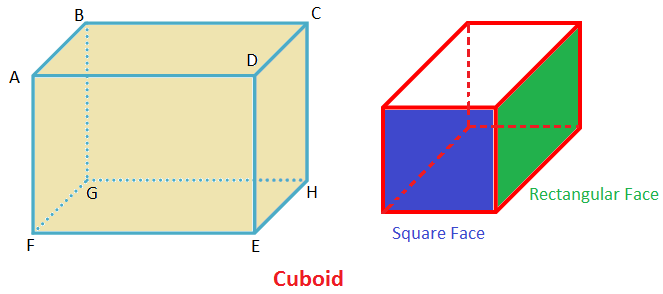
figure below shows two cuboids.
Consider the cuboid on the left. It has
1. Six rectangular faces, namely ABCD, EFGH, ABGF, CDEH, ADEF and BGHC. Its opposite faces are congruent.
2. Twelve edges, namely AB,BC, CD, DA, FG, HE, EF, AF, BG, CH and DE. The edges AB, CD, FG, EH are equal; the edges BC, AD, GH, EF are equal; the edges AF, BG, CH, DE are equal.
3. Eight Corners (or vertices), namely A, B, C, D, E, F, G and H.
4. Three dimensions: Length (l) = FE, breadth (b) = FG and height (h) = AF.
5. Four diagonals, namely AH, FC, BE and GD which are all equal. These are line segments joining opposite corners (not on the same face).
Note: The dimensions of a cuboid are a cm × b cm × c cm means the length = a cm, breadth = b cm and height = c cm.
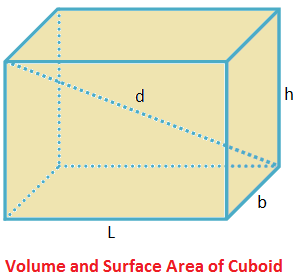
Volume of a Cuboid (V) = l × b × h
Total surface Are of a Cuboid (S) = 2(lb + bh +hl)
Diagonal a Cuboid (d) = \(\sqrt{\mathrm{l^{2} + b^{2} + h^{2}}}\)
Where l = Length, b = breadth and h = height.
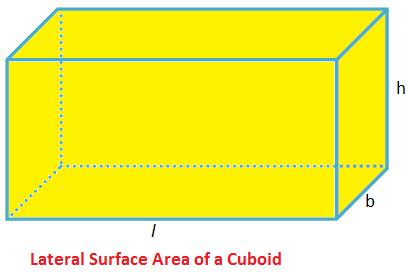
Area of the Four Walls of a Room (Lateral Surface Area of a Cuboid)
Rooms area examples of cuboids.
Are of the four walls of a room = sum of the four vertical (or lateral) faces
= 2(l + b)h
Where l = Length, b = breadth and h = height.
Problems on Volume and Surface Area of Cuboid:
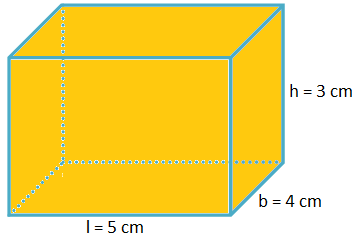
1. A cuboid has three mutually perpendicular edges measuring 5 cm, 4 cm and 3 cm. Find (i) its volume, (ii) its surface area, and (iii) the length of the diagonal.
Solution:
Three mutually perpendicular edges are the length, breadth and height.
Length = l = 5 cm, breadth = b = 4 cm, height = h = 3 cm.
Therefore, (i) Volume = l × b × h = 5 × 4 × 3 cm3 = 60 cm3;
(ii) Surface area = 2(lb + bh + hl) = 2(5 × 4 + 4 × 3 + 3 × 5) cm2
= 2(20 + 12 + 15) cm2
= 94 cm2;
(iii) Length of a diagonal = \(\sqrt{\mathrm{l^{2} + b^{2} + h^{2}}}\)
= \(\sqrt{\mathrm{5^{2} + 4^{2} + 3^{2}}}\) cm
= \(\sqrt{50}\) cm
= 5√2 cm.
2. The length, breadth and volume of a cuboid are 8 cm, 6 cm and 192 cm3 respectively. Find its (i) height, (ii) surface area, and (iii) lateral surface area.
Solution:
Let the height = h.
Then, volume = l × b × h
⟹ 192 cm3 = 8 cm × 6 cm × h
⟹ h = \(\frac{192 cm^{3}}{8 × 6 cm^{2}}\)
⟹ h = \(\frac{192 cm^{3}}{48 cm^{2}}\)
⟹ h = 4 cm.
Therefore, (i) height = 4 cm.
(ii) Surface area = 2(lb + bh + hl)
= 2(8 × 6 + 6 × 4 + 4 × 8) cm2
= 2(48 + 24 + 32) cm2
= 208 cm2
(iii) Lateral surface area = 2(l + b)h
= 2(8 + 6) × 4 cm2
= 2(14) × 4 cm2
= 28 × 4 cm2
= 112 cm2
You might like these
-
Problems on Right Circular Cylinder | Application Problem | Diagram
Problems on right circular cylinder. Here we will learn how to solve different types of problems on right circular cylinder. 1. A solid, metallic, right circular cylindrical block of radius 7 cm and height 8 cm is melted and small cubes of edge 2 cm are made from it.
-
Hollow Cylinder | Volume |Inner and Outer Curved Surface Area |Diagram
We will discuss here about the volume and surface area of Hollow Cylinder. The figure below shows a hollow cylinder. A cross section of it perpendicular to the length (or height) is the portion bounded by two concentric circles. Here, AB is the outer diameter and CD is the
-
Right Circular Cylinder | Lateral Surface Area | Curved Surface Area
A cylinder, whose uniform cross section perpendicular to its height (or length) is a circle, is called a right circular cylinder. A right circular cylinder has two plane faces which are circular and curved surface. A right circular cylinder is a solid generated by the
-
Cylinder | Formule for the Volume and the Surface Area of a Cylinder
A solid with uniform cross section perpendicular to its length (or height) is a cylinder. The cross section may be a circle, a triangle, a square, a rectangle or a polygon. A can, a pencil, a book, a glass prism, etc., are examples of cylinders. Each one of the figures shown
-
Cross Section | Area and Perimeter of the Uniform Cross Section
The cross section of a solid is a plane section resulting from a cut (real or imaginary) perpendicular to the length (or breadth of height) of the solid. If the shape and size of the cross section is the same at every point along the length (or breadth or height) of the
From Volume and Surface Area of Cuboid to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.