Trigonometric Identities

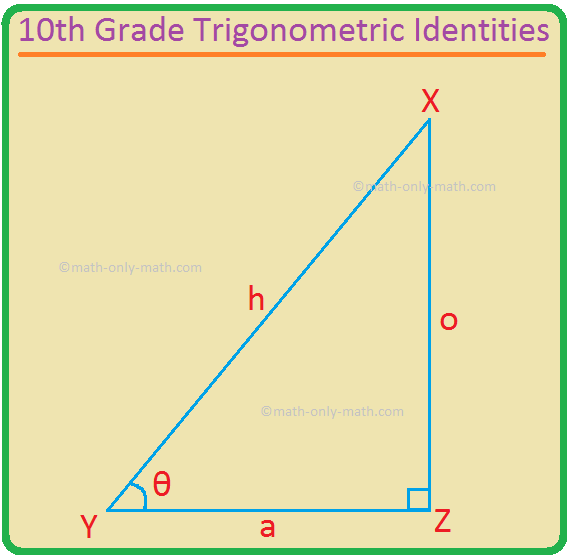
XYZ is a right-angled triangle in which ∠XZY = 90° and ∠XYZ = θ, which in an acute angle.

We know,

sin θ = $\frac{\textrm{Opposite}}{\textrm{Hypotenuse}}$ = $\frac{o}{h}$;

cos θ = $\frac{\textrm{Adjacent}}{\textrm{Hypotenuse}}$ = $\frac{a}{h}$;

tan θ = $\frac{\textrm{Opposite}}{\textrm{Adjacent}}$ = $\frac{o}{a}$;

csc θ = $\frac{\textrm{Hypotenuse}}{\textrm{Opposite}}$ = $\frac{h}{o}$;

sec θ = $\frac{\textrm{Hypotenuse}}{\textrm{Adjacent}}$ = $\frac{h}{a}$;

cot θ = $\frac{\textrm{Adjacent}}{\textrm{Opposite}}$ = $\frac{a}{o}$.

Let’s multiply sin θ and csc θ

sin θ ∙ csc θ = $\frac{o}{h}$ × $\frac{h}{o}$ = 1

Therefore, csc θ = $\frac{1}{sin θ}$

Now, multiply cos θ and sec θ

cos θ ∙ sec θ = $\frac{a}{h}$ × $\frac{h}{a}$ = 1

Therefore, sec θ = $\frac{1}{cos θ}$

Again, multiply tan θ and cot θ

tan θ ∙ cot θ = $\frac{o}{a}$ × $\frac{a}{a}$ = 1

Therefore, cot θ = $\frac{1}{tan θ}$

Let’s divide sin θ by cos θ

sin θ ÷ cos θ = $\frac{sin θ}{cos θ}$ = $\frac{\frac{o}{h}}{\frac{a}{h}}$ = $\frac{o}{a}$ = tan θ.

Therefore, tan θ = $\frac{sin θ}{cos θ}$.

Similarly, divide cos θ by sin θ

cos θ ÷ sin θ = $\frac{cos θ}{sin θ}$ = $\frac{\frac{a}{h}}{\frac{o}{h}}$ = $\frac{a}{o}$ = cot θ.

Therefore, cot θ = $\frac{cos θ}{sin θ}$.

If a relation of equality between two expressions involving trigonometric ratios of an angle θ holds true for all values of θ then the equality is called a trigonometric identity. But it holds true only for some values of θ, the equality gives a trigonometric equation. There are a number of fundamental trigonometric identities.

I.  sin$^{2}$ θ + cos$^{2}$ θ = 1

We have, sin θ = $\frac{o}{h}$ and cos θ = $\frac{a}{h}$.

Therefore, sin$^{2}$ θ + cos$^{2}$ θ = $\frac{o^{2}}{h^{2}}$ + $\frac{a^{2}}{h^{2}}$.

                                       = $\frac{o^{2} + a^{2}}{h^{2}}$

                                       = $\frac{h^{2}}{h^{2}}$; [Since, in the right-angled ∆XYZ, o$^{2}$ + a$^{2}$ = h$^{2}$ (by Pythagoras’ Theorem)]

                                        = 1.

Therefore, sin$^{2}$ θ + cos$^{2}$ θ = 1.

Consequently, 1 - sin$^{2}$ θ = cos$^{2}$ θ and 1 - cos$^{2}$ θ = sin$^{2}$ θ.

II. sec$^{2}$ θ - tan$^{2}$ θ = 1

We have, sec θ = $\frac{h}{a}$ and tan θ = $\frac{o}{a}$.

Therefore, sec$^{2}$ θ - tan$^{2}$ θ = $\frac{h^{2}}{a^{2}}$ - $\frac{o^{2}}{a^{2}}$.

                                      = $\frac{h^{2} - o^{2}}{a^{2}}$

                                      = $\frac{a^{2}}{a^{2}}$; [Since, in the right-angled ∆XYZ, o$^{2}$ + a$^{2}$ = h$^{2}$ ⟹ h$^{2}$ - o$^{2}$ = a$^{2}$ (by Pythagoras’ Theorem)]

                                      = 1.

Therefore, sec$^{2}$ θ - tan$^{2}$ θ = 1.

Consequently, 1 + tan$^{2}$ θ = sec$^{2}$ θ and sec$^{2}$ θ - 1 = tan$^{2}$ θ.

III. csc$^{2}$ θ - cot$^{2}$ θ = 1

We have, csc θ = $\frac{h}{o}$ and cot θ = $\frac{a}{o}$.

Therefore, csc$^{2}$ θ - cot$^{2}$ θ = $\frac{h^{2}}{o^{2}}$ - $\frac{a^{2}}{o^{2}}$.

                                       = $\frac{h^{2} - a^{2}}{o^{2}}$

                                       = $\frac{o^{2}}{o^{2}}$; [Since, in the right-angled ∆XYZ, o$^{2}$ + a$^{2}$ = h$^{2}$ ⟹ h$^{2}$ - a$^{2}$ = o$^{2}$ (by Pythagoras’ Theorem)]

                                       = 1.

Therefore, csc$^{2}$ θ - cot$^{2}$ θ = 1.

Consequently, 1 + cot$^{2}$ θ = csc$^{2}$ θ and csc$^{2}$ θ - 1 = cot$^{2}$ θ.

These three trigonometric identities are also called Pythagorean identities.

Note: The equalities csc θ = $\frac{1}{sin θ}$, sec θ = $\frac{1}{cos θ}$, cot θ = $\frac{1}{tan θ}$, tan θ = $\frac{sin θ}{cos θ}$ and cot θ = $\frac{cos θ}{sin θ}$ are holds for all values of θ. Therefore, these equalities are trigonometric identities.

Thus, we have the following trigonometric identities.

Table of Trigonometric Identities

1. csc θ = $\frac{1}{sin θ}$,

2. sec θ = $\frac{1}{cos θ}$,

3. cot θ = $\frac{1}{tan θ}$,

4. tan θ = $\frac{sin θ}{cos θ}$,

5. cot θ = $\frac{cos θ}{sin θ}$

6. sin$^{2}$ θ + cos$^{2}$ θ = 1; 1 - sin$^{2}$ θ = cos$^{2}$ θ, 1 - cos$^{2}$ θ = sin$^{2}$ θ.

7. sec$^{2}$ θ - tan$^{2}$ θ = 1; 1 + tan$^{2}$ θ = sec$^{2}$ θ; sec$^{2}$ θ - 1 = tan$^{2}$ θ.

8. csc$^{2}$ θ - cot$^{2}$ θ = 1

9. 1 + cot$^{2}$ θ = csc$^{2}$ θ,

10. csc$^{2}$ θ - 1 = cot$^{2}$ θ.

Solved Examples on Trigonometric Identities:

1. Prove that sin$^{4}$ θ + cos$^{4}$  θ + 2 sin$^{2}$ θ ∙ cos$^{2}$  θ = 1

Solution:

LHS = sin$^{4}$ θ + cos$^{4}$  θ + 2 sin$^{2}$ θ ∙ cos$^{2}$  θ

       = (sin$^{2}$ θ)$^{2}$ + (cos$^{2}$  θ)$^{2}$ + 2 sin$^{2}$ θ ∙ cos$^{2}$  θ

       = (sin$^{2}$ θ + cos$^{2}$ θ)$^{2}$

       = 1$^{2}$; [Since, sin$^{2}$ θ + cos$^{2}$ θ = 1]

       = 1 = RHS. (Proved).

How to Solve Trigonometric Identities Proving Problems?

2. Show that sec θ - cos θ = sin θ tan θ

Solution:

LHS =  sec θ - cos θ

      = $\frac{1}{cos θ}$ - cos θ

      = \(\frac{1 - cos^{2} θ}{cos θ}\)

      = \(\frac{sin^{2} θ}{cos θ}\);  [Since, sin$^{2}$ θ + cos$^{2}$ θ = 1]

      = sin θ ∙ \(\frac{sin θ}{cos θ}\)

      = sin θ ∙ tan θ = RHS. (Proved)

3. Prove that 1 - $\frac{cos^{2} A}{1 + sin A}$ = sin A

Solution:

LHS = 1 - $\frac{cos^{2} A}{1 + sin A}$

       = 1 - $\frac{1 - sin^{2} A}{1 + sin A}$; [cos$^{2}$ θ = 1 - sin$^{2}$ θ]

       = 1 - $\frac{(1 + sin A)(1 – sin A)}{1 + sin A}$

       = 1 – (1 – sin A)

       = 1 – 1 + sin A

       = sin A = RHS. (Proved).

Verifying Trigonometric Identities & Equations

4. Prove that $\frac{sin A}{1 + cos A}$ + $\frac{sin A}{1 - cos A}$ = 2 csc A.

Solution:

LHS = $\frac{sin A}{1 + cos A}$ + $\frac{sin A}{1 - cos A}$

       = $\frac{sin A(1 – cos A) + sin A(1 + cos A)}{(1 + cos A)(1 – cos A)}$

       = $\frac{sin A – sin A ∙ cos A + sin A + sin A ∙ cos A)}{1 - cos^{2} A}$

       = $\frac{2 sin A}{sin^{2} A}$; [Since, 1 - cos$^{2}$ A = sin$^{2}$ A]

       = $\frac{2}{sin A}$

       = 2 ∙ $\frac{1}{sin A}$; [Since, csc A = $\frac{1}{sin A}$]

       = RHS. (Proved).

Proving Trigonometric Identities Practice Problems Online

5. Prove that $\frac{sin A}{1 + cos A}$ = $\frac{1 – cos A}{sin A}$.

Solution:

LHS = $\frac{sin A}{1 + cos A}$

       = $\frac{sin A}{1 + cos A}$ ∙ $\frac{1 - cos A}{1 - cos A}$

       = $\frac{sin A(1 - cos A)}{1 - cos^{2} A}$

       = $\frac{sin A(1 - cos A)}{sin^{2} A}$; [Since 1 - cos$^{2}$ θ = sin$^{2}$ θ]

       = $\frac{1 - cos A}{sin A}$ = RHS. (Proved).

Trigonometry Problems and Questions with Solutions

6. Prove that $\sqrt{\frac{1 + sin θ}{1 - sin θ}}$ = sec θ +tan θ.

Solution:

LHS = $\sqrt{\frac{1 + sin θ}{1 - sin θ}}$

       = $\sqrt{\frac{(1 + sin θ) (1 + sin θ)}{(1 - sin θ)(1 + sin θ)}}$

       = $\sqrt{\frac{(1 + sin θ)^{2}}{1 – sin^{2} θ}}$

       = $\sqrt{\frac{(1 + sin θ)^{2}}{cos^{2} θ}}$; [Since 1 - sin$^{2}$ θ = cos$^{2}$ θ]

       = $\frac{1 + sin θ}{cos θ}$

       = $\frac{1}{cos θ}$ + $\frac{sin θ}{cos θ}$

       = secθ + tan θ = RHS. (Proved).

Trigonometric identities problems for class 10

7. Prove that tan$^{2}$ A – tan$^{2}$ B = $\frac{sin^{2} A - sin^{2} B}{cos^{2} A ∙ cos^{2} B}$ = sec$^{2}$ A - sec$^{2}$ B

Solution:

LHS = tan$^{2}$ A – tan$^{2}$ B

       = $\frac{sin^{2} A}{cos^{2} A}$ - $\frac{ sin^{2} B}{cos^{2} B}$

       = $\frac{sin^{2} A ∙ cos^{2} B - sin^{2} B ∙ cos^{2} A}{cos^{2} A ∙ cos^{2} B}$

       = $\frac{sin^{2} A (1 - sin^{2} B) - sin^{2} B(1 - sin^{2} A)}{cos^{2} A ∙ cos^{2} B}$; [Since, cos² B = 1 - sin² B and cos² A = 1 - sin² A]

       = $\frac{sin^{2} A  - sin^{2} A  sin^{2} B - sin^{2} B + sin^{2} B sin^{2} A}{cos^{2} A ∙ cos^{2} B}$;

        = $\frac{sin^{2} A - sin^{2} B}{cos^{2} A ∙ cos^{2} B}$ = MHS

        = $\frac{(1 - cos^{2} A) - (1 - cos^{2} B)}{cos^{2} A ∙ cos^{2} B}$; [Since, sin² A = 1 - cos² A and sin² B = 1 - cos² B]

        = $\frac{cos^{2} B - cos^{2} A}{cos^{2} A ∙ cos^{2} B}$

        = $\frac{cos^{2} B}{cos^{2} A ∙ cos^{2} B}$ - $\frac{cos^{2} A}{cos^{2} A ∙ cos^{2} B}$

        = $\frac{1}{cos^{2} A}$ - $\frac{1}{cos^{2} B}$

        = sec$^{2}$ A – sec$^{2}$ B = RHS. (Proved)

Again, 

LHS = tan$^{2}$ A – tan$^{2}$ B

       = (sec$^{2}$ A – 1) – (sec$^{2}$ B – 1); [Since, tan$^{2}$ θ = sec$^{2}$ θ – 1 ]

       = sec$^{2}$ A – 1 – (sec$^{2}$ B +1

       = sec$^{2}$ A – sec$^{2}$ B = RHS. (Proved).

Solving Trigonometric Equations using Trigonometric Identities

8. Prove that tan$^{2}$ θ - sin$^{2}$ θ = tan$^{2}$ θ ∙ sin$^{2}$ θ

Solution:

LHS = tan$^{2}$ θ - sin$^{2}$ θ

       = tan$^{2}$ θ - $\frac{sin^{2} θ}{cos^{2} θ}$ ∙ cos$^{2}$

       = tan$^{2}$ θ - tan$^{2}$ θ ∙ cos$^{2}$

       = tan$^{2}$ θ(1 - cos$^{2}$)

       = tan$^{2}$ θ ∙ sin$^{2}$ θ = RHS. (Proved).

List of trigonometric identities Problems

9. Prove that 1 + $\frac{cot^{2} θ}{1 + csc θ}$ = csc θ

Solution:

LHS = 1 + $\frac{cot^{2} θ}{1 + csc θ}$

       = 1 + $\frac{csc^{2} θ - 1}{1 + csc θ}$

       = 1 + $\frac{(csc θ + 1)(csc θ – 1)}{1 + csc θ}$

       = 1 + (csc θ – 1)

       = 1 + csc θ – 1

       = csc θ = RHS. (Proved).

10. Prove that $\frac{sec θ - )}{sec θ + 1}$ = (cot θ – csc θ)$^{2}$.

Solution:

LHS = $\frac{sec θ - 1}{sec θ + 1}$

       = $\frac{sec θ - 1}{sec θ + 1}$ ∙ $\frac{sec θ - 1}{sec θ - 1}$

       = $\frac{(sec θ - 1)^{2}}{sec^{2} θ - 1}$

       = $\frac{(sec θ - 1)^{2}}{tan^{2} θ}$; [Since sec$^{2}$ θ – 1 = tan$^{2}$ θ]

       = $(\frac{sec θ - 1}{tan θ})^{2}$

       = $(\frac{\frac{1}{cos θ} - 1}{\frac{sin θ }{cos θ} })^{2}$

       = $(\frac{1 – cos θ}{cos θ} ∙ \frac{cos θ}{sin θ})^{2}$

       = $(\frac{1 – cos θ}{sin θ})^{2}$

       = $(\frac{1}{sin θ} - \frac{cos θ}{sin θ})^{2}$

       = (csc θ – cot θ)$^{2}$

       = (cot θ – csc θ)$^{2}$ = RHS. (Proved).

Proving Trigonometric Identities

11. Prove that $\frac{sin A}{cot A + csc A}$ = 2 + $\frac{sin A}{cot A - csc A }$

Solution:

LHS = $\frac{sin A}{cot A + csc A}$

       = $\frac{sin A(cot A - csc A)}{(cot A + csc A)(cot A - csc A)}$

       = $\frac{sin A ∙ cot A – sin A ∙ csc A}{cot^{2} A – csc^{2} A}$

       = $\frac{sin A ∙ \frac{cos A}{sin A} – 1}{-1}$; [since, sin θ csc θ = 1, csc$^{2}$ θ – cot$^{2}$  θ = 1]

       = $\frac{cos A - 1}{-1}$

       = 1 – cos A

RHS = 2 + $\frac{sin A}{cot A - csc A}$

        = 2 + $\frac{sin A}{ cot A - csc A}$ ∙ $\frac{(cot A + csc A)}{(cot A + csc A)}$

        = 2 + $\frac{sin A(cot A + csc A)}{cot^{2} A – csc^{2} A}$

        = 2 + $\frac{sin A(\frac{cos A}{sin A} + \frac{1}{sin A})}{-1}$

        = 2 + $\frac{cos A + 1}{-1}$

        = 2 – (cos A + 1)

        = 2 – cos A – 1

        = 1 – cos A

Therefore, LHS = RHS. (Proved).

Alternative Method

The identity is established if we can prove that

$\frac{sin A}{cot A + csc A}$ - $\frac{sin A}{cot A - csc A }$ = 2

Now, here  

LHS = $\frac{sin A}{cot A + csc A}$ - $\frac{sin A}{cot A - csc A }$

       = $\frac{sin A(cot A - csc A) – sin A(cot A + csc A)}{( cot A + csc A)(cot A - csc A)}$

       = $\frac{sin A ∙ cot A – sin A ∙ csc A – sin A ∙ cot A – sin A ∙ csc A}{(cot A + csc A)(cot A - csc A)}$

       = $\frac{–2 sin A ∙ csc A}{cot^{2} A – csc^{2} A}$

       = $\frac{–2}{-1 }$; [Since sin θ csc θ = 1, csc$^{2}$ θ – cot$^{2}$  θ = 1]

       = 2 = RHS. (Proved)

Problems on Evaluation using Trigonometric Identities:

12. If sin θ + csc θ = 2, find the value of sin$^{10}$ θ + csc$^{11}$ θ

Solution:

Given that, sin θ + csc θ = 2 ……………. (i)

⟹ sin θ + $\frac{1}{ sin θ}$ = 2

⟹ $\frac{ sin^{2} θ + 1}{sin θ }$ = 2

⟹ sin$^{2}$ θ + 1= 2 sin θ

⟹ sin$^{2}$ θ - 2 sin θ + 1 = 0

⟹ (sin θ - 1)$^{2}$ = 0

⟹ sin θ - 1 = 0

⟹ sin θ = 1

⟹ csc θ = $\frac{1}{ sin θ}$ = $\frac{1}{ 1}$ = 1

Therefore, csc θ = 1.

Now, sin$^{10}$ θ + csc$^{11}$ θ

= 1$^{10}$ + 1$^{11}$

= 1 + 1

= 2.

13. If sec θ – tan θ = $\frac{1}{3}$, find the value of sec A and tan A.

Solution:

Given, sec θ – tan θ = $\frac{1}{3}$ ………… (i)

We know that the Pythagorean identity, sec$^{2}$ θ - tan$^{2}$ θ = 1.

                   ⟹ (sec θ + tan θ)(sec θ - tan θ) = 1

                   ⟹ (sec θ + tan θ) ∙ $\frac{1}{3}$ = 1, [Given sec θ – tan θ = $\frac{1}{3}$]

                   ⟹ sec θ + tan θ = 3 ……….. (ii)

Now adding (i) and (ii) we get

                       2 sec θ = $\frac{1}{3}$ + 3

                   ⟹ 2 sec θ = $\frac{10}{3}$

                   ⟹ sec θ = $\frac{10}{3}$ ∙ $\frac{1}{2}$

                   ⟹ sec θ = $\frac{5}{3}$

Therefore, sec θ = $\frac{5}{3}$

Putting the value of sec θ = $\frac{5}{3}$ in (ii), we get

$\frac{5}{3}$ + tan θ = 3

⟹ tan θ = 3 - $\frac{5}{3}$

⟹ tan θ = $\frac{4}{3}$

Therefore, tan θ = $\frac{4}{3}$.

14. If tan A + sec A = $\frac{2}{\sqrt{3}}$, find the value of sin A

Solution:

Given that, tan A + sec A = $\frac{2}{\sqrt{3}}$ ……………….. (i)

We know the Pythagorean trigonometric identity,

       sec$^{2}$ A - tan$^{2}$ A = 1.

⟹ (sec A + tan A)(sec A – tan A) = 1

⟹ $\frac{2}{\sqrt{3}}$(sec A – tan A) = 1; [given , tan A + sec A = $\frac{2}{\sqrt{3}}$]

⟹ sec A – tan A = $\frac{\sqrt{3}}{2}$ ……………….. (ii)

Solving these two equations we get,

     2 sec A = $\frac{2}{\sqrt{3}}$ + $\frac{\sqrt{3}}{2}$

 ⟹ 2 sec A = $\frac{4 + 3}{2\sqrt{3}}$

 ⟹ 2 sec A = $\frac{7}{2\sqrt{3}}$

⟹ sec A = $\frac{7}{4\sqrt{3}}$ ……………….. (iii)

Putting the value of sec A = $\frac{7}{4\sqrt{3}}$ in (i) we get,

     tan A + $\frac{7}{4\sqrt{3}}$ = $\frac{2}{\sqrt{3}}$

⟹ tan A = $\frac{2}{\sqrt{3}}$ - $\frac{7}{4\sqrt{3}}$

⟹ tan A = $\frac{8 - 7}{4\sqrt{3}}$

⟹ tan A = $\frac{1}{4\sqrt{3}}$……………….. (iv)

Now dividing (iv) by (iii) we get,

$\frac{tan A}{sec A}$ = $\frac{1}{7}$

⟹ sin A = $\frac{1}{7}$

Therefore, sin A = $\frac{1}{7}$.

Problems on establishing conditional results

15. If cos A + sin A = $\sqrt{2}$ cos A, prove that cos A - sin A = $\sqrt{2}$ sin A.

Solution:

Let cos A - sin A = k. Now,

(cos A + sin A)$^{2}$ + (cos A - sin A)$^{2}$ = cos$^{2}$ A + sin$^{2}$ A + 2 cos A ∙ sin A + cos$^{2}$ A + sin$^{2}$ A - 2 cos A ∙ sin A

                                            = 1 + 2 cos A sin A + 1 - 2 cos A sin A

                                            = 2

Therefore, ($\sqrt{2}$ cos A)$^{2}$ + k$^{2}$ = 2

⟹ k$^{2}$ = 2 - ($\sqrt{2}$ cos A)$^{2}$ 

⟹ k$^{2}$ = 2 - 2cos$^{2}$ A

⟹ k$^{2}$ = 2(1 - cos$^{2}$ A)

⟹ k$^{2}$ = 2sin$^{2}$ A; [Since, sin$^{2}$ θ + cos$^{2}$ θ = 1]

⟹ k = $\sqrt{2}$ sin A

⟹ cos A - sin A = $\sqrt{2}$ sin A. (Proved).

10th Grade Math

From Trigonometric Identities to HOME PAGE