Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Subtracting 2-digit Numbers with Borrowing (Regrouping)
Here we will learn subtracting 2-digit numbers with borrowing. The subtractions with borrowing are solved step-by-step in four different ways.
When we need to subtract bigger number from a smaller number in ones place, we regroup tens into ones.
Regrouping
We can write a 2-digit number in different ways by regrouping tens and ones.
16 can be written as
23 can be written as
Let us understand this with the help of an example.
A shopkeeper sells bananas. He has 6 bunches of 10's and 5 single bananas.
Nairitee wants to buy 37 bananas from the shopkeeper. The shopkeeper gives her 3 bunches of 10's and breaks one bunch of 10's to give 7 bananas.
The shopkeeper is now left with how many bananas?
Column Method
Arrange the numbers in columns and subtract. In ones place, 5 is smaller than 7. We cannot take away 7 from 5. So, we break one ten into 10 ones. Now we have, 15 ones in ones place and 5 tens in tens place.
|
15 ones - 7 ones = 8 We write 8 in ones place. Subtract 3 tens from 5 tens. 5 tens - 3 tens = 2 tens Write 2 in tens place. |
So, 65 - 37 = 28
Worked-out examples on subtracting 2-digit numbers with borrowing:
1. Subtract 9 from 15.
Solution:
T O
1 5
- 9
Since, 5 < 9, so 9 cannot be subtracted from 5. So, 1 ten, i.e., 10 ones is borrowed from the digit 1 of tens place. Now one ten, i.e., 10 ones are added to 5 ones to make it 15 ones. Now 15 ones – 9 ones = 6 ones.
Therefore, 15 – 9 = 6
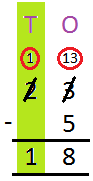
2. Subtract 37
from 65
Solution:
The numbers are placed in column form, with the smaller number 37 written under the greater number 65.
T O
1 T → 10
6 5
- 3 7
2 8
(i) first ones are subtracted as 5 < 7 or 7 > 5. So, 7 cannot be subtracted from 5.
(ii) Now 1 ten is borrowed from 6 tens leaving 5 tens there.
(iii) 1 ten = 10 ones. So, 10 ones are added to 5 ones making the sum 15 ones
(iv) 7 ones are subtracted from 15 ones i.e., 15 ones – 7 ones = 8 ones. This 8 is written in one’s column.
(v) Now tens are subtracted. At ten’s place there are 5 tens left. So 5 tens – 3 tens = 2 tens. So, 2 is written in ten’s column.
(vi) Therefore, 65 – 37 = 28.
3. Subtract 28 from 83
Solution:
The smaller number 28 is written under greater number 83 in column form and ones are subtracted first, then the tens.
T O
1 T → 10
8 3
- 2 8
5 5
(i) 3 < 8, so 1 ten, i.e., 10 ones are borrowed from 8 tens with 7tens remaining there.
(ii) Now, 1 ten + 3 = 10 + 3 = 13 ones. So, 13 ones – 8 ones = 5 ones.
(iii) 7 tens – 2 tens = 5 tens.
Therefore, 83 – 28 = 55
4. Subtract 69 from 92
Solution:
The smaller number 69 is written under greater number 92 in column form and ones are subtracted first, then the tens.
T O
1 T → 10
9 2
- 6 9
2 3
(i) 10 + 2 = 12; 12 O – 9 O = 3 O
(ii) 8 T – 6 T = 2 T
Therefore, 92 – 69 = 23
Subtraction with Borrowing:
5. Let us subtract 5 from 23.
|
Step I: Arrange the numbers into tens and ones. | |
|
Step II: We cannot subtract 5 from 3. So, borrow 1 ten from the tens column. 1 ten = 10 ones. Take these 10 ones to the ones column. This gives: 10 + 3 = 13 ones 13 – 5 = 8 | |
|
Step III: Subtract the tens. Now since we borrowed 1 ten, we are left with 1 ten in the tens column. |
Thus, 23 – 5 = 18
6. Let us subtract 37 from 53.
|
Step I: Arrange the numbers into tens and ones. | |
|
Step II: We cannot subtract 7 from 3. So, borrow 1 ten from the tens column. 1 ten = 10 ones. Take these 10 ones to the ones column. This gives: 10 + 3 = 13 ones 13 – 7 = 6 | |
|
Step III: Since we have borrowed 1 ten from 5 tens, we are left with 4 tens. Now subtract 3 tens from 4 tens. 4 – 3 = 1 |
Thus, 53 – 37 = 16
Questions and Answers on Subtracting 2-Digit Numbers with Borrowing (Regrouping):
1. Regrouping the tens and ones.
|
(i) |
24 = |
2 |
tens + |
4 |
ones = |
1 |
ten + |
14 |
ones |
|
(ii) |
57 = |
___ |
tens + |
___ |
ones = |
4 |
tens + |
___ |
ones |
|
(iii) |
64 = |
___ |
tens + |
___ |
ones = |
___ |
tens + |
14 |
ones |
|
(iv) |
48 = |
___ |
tens + |
___ |
ones = |
3 |
tens + |
___ |
ones |
2. Subtracting 1-digit number from 2-digit number with regrouping.
(i) 38 - 9 = _____
(ii) 62 - 7 = _____
(iii) 44 - 6 = _____
(iv) 67 - 8 = _____
(v) 75 - 7 = _____
(vi) 94 - 8 = _____
(vii) 74 - 5 = _____
(viii) 51 - 2 = _____
(ix) 95 - 6 = _____
(x) 42 - 3 = _____
(xi) 53 - 4 = _____
(xii) 62 - 4 = _____
(xiii) 67 - 8 = _____
(xiv) 32 - 5 = _____
(xv) 22 - 9 = _____
(xvi) 93 - 3 = _____
Answers:
2. (i) 29
(ii) 55
(iii) 38
(iv) 59
(v) 68
(vi) 86
(vii) 69
(viii) 49
(ix) 89
(x) 39
(xi) 49
(xii) 58
(xiii) 59
(xiv) 27
(xv) 13
(xvi) 90
3. Subtracting 2-digit number with regrouping.
(i) 80 - 17 = _____
(ii) 38 - 29 = _____
(iii) 71 - 34 = _____
(iv) 47 - 19 = _____
(v) 86 - 27 = _____
(vi) 65 - 47 = _____
(vii) 51 - 25 = _____
(viii) 62 - 37 = _____
(ix) 73 - 57 = _____
(x) 94 - 46 = _____
(xi) 46 - 28 = _____
(xii) 56 - 27 = _____
(xiii) 57 - 19 = _____
(xiv) 31 - 24 = _____
(xv) 41 - 16 = _____
(xvi) 53 - 29 = _____
Answers:
3. (i) 63
(ii) 9
(iii) 37
(iv) 28
(v) 59
(vi) 18
(vii) 26
(viii) 25
(ix) 16
(x) 48
(xi) 18
(xii) 29
(xiii) 38
(xiv) 7
(xv) 25
(xvi) 24
4. Subtract.
|
(i) |
- |
T O 6 3 4 6 __________ |
(ii) |
- |
T O 3 4 2 9 __________ |
|
(iii) |
- |
T O 9 3 5 8 __________ |
(iv) |
- |
T O 7 6 5 9 __________ |
|
(v) |
- |
T O 3 2 1 5 __________ |
(vi) |
- |
T O 4 4 3 6 __________ |
|
(vii) |
- |
T O 5 2 2 8 __________ |
(viii) |
- |
T O 3 2 1 9 __________ |
|
(ix) |
- |
T O 8 3 6 9 __________ |
(x) |
- |
T O 7 5 2 6 __________ |
Answers:
4. (i) 17
(ii) 5
(iii) 35
(iv) 17
(v) 17
(vi) 8
(vii) 24
(viii) 13
(ix) 14
(x) 49
From Subtracting 2-digit Numbers with Borrowing (Regrouping) to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
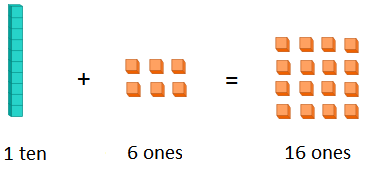
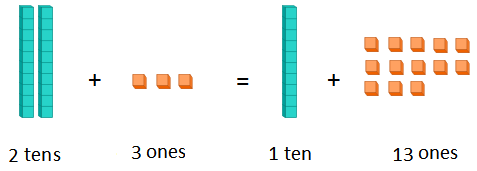


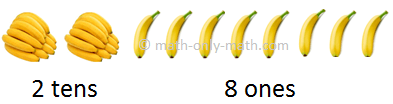

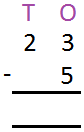
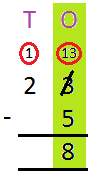
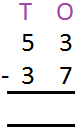
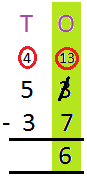


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.