Subscribe to our YouTube channel for the latest videos, updates, and tips.
Lateral Surface Area of a Cuboid
Here we will learn how to solve the application problems on lateral surface area of a cuboid using the formula.
Formula for finding the lateral surface area of a cuboid
Area of a Rooms is example of cuboids.
Are of the four walls of a room = sum of the four vertical (or lateral) faces
= 2(l + b)h
Where l = Length, b = breadth and h = height.
Therefore, lateral surface area of a cuboid = 2(l + b)h
Problems on Lateral Surface Area of a Cuboid:
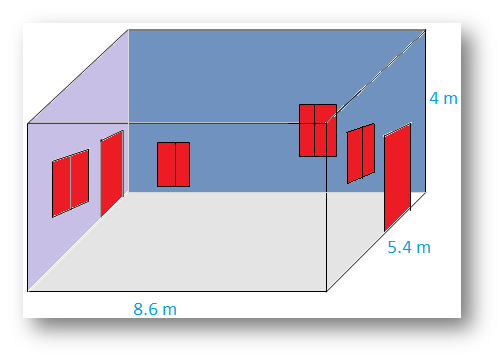
The dimensions of a cubical room are 8.6 m × 5.4 m × 4 m. The room has two doors each measuring 2 m by 1 m and four windows each measuring 1 m by 1 m. What will be the cost of plastering the four walls and the ceiling at RS 65 per m2?
Solution:
The total area of the four walls
= Lateral surface area of the cuboid
= 2(l + b)h
= 2(86 + 5.4) × 4 m2
= 112 m2.
The area of the ceiling = l × b
= 8.6 × 5.4 m2
= 46.44 m2
The sum of the areas of the two doors and the four windows
= 2(2 × 1) m2 + 4(1 × 1) m2
= 8 m2
Therefore, the total area to be plastered = (112 + 46.44 - 8) m2
= 150.44 m2
Therefore, the cost of plastering = 150.44 × Rs. 65
= Rs. 9778.60.
From Lateral Surface Area of a Cuboid to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
8 Times Table | Multiplication Table of 8 | Read Eight Times Table
May 18, 25 04:33 PM
In 8 times table we will memorize the multiplication table. Printable multiplication table is also available for the homeschoolers. 8 × 0 = 0 8 × 1 = 8 8 × 2 = 16 8 × 3 = 24 8 × 4 = 32 8 × 5 = 40 -
Worksheet on Average | Word Problem on Average | Questions on Average
May 17, 25 05:37 PM
In worksheet on average interest we will solve 10 different types of question. Find the average of first 10 prime numbers. The average height of a family of five is 150 cm. If the heights of 4 family -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed. -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 16, 25 11:13 AM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.