Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Fraction as a Part of a Whole
In our daily life we often hear the words like half, quarter, one third etc. These type of words show that they are part of a thing. When we divide anything into equal parts each part is called a fraction of the whole.
A whole can either be a region (an object) or a collection (group of objects).
How is fraction as a part of a whole?
We know, a fraction means a part. So, fraction is the part of a whole object.
Thus, a fraction is the part of a collection or collections of objects.
A fraction is a part of a whole number say 1, 2, 3, 4, ……. 150 ……. etc.
Thus, a number which is not a whole number is known as a fractional number.
For example; 1/2, 1/3, 2/3, 3/4, 5/6, …………… are fractional numbers.
Pictures of fraction as a part of a whole:
Fractions of a Region:
1. Halves -
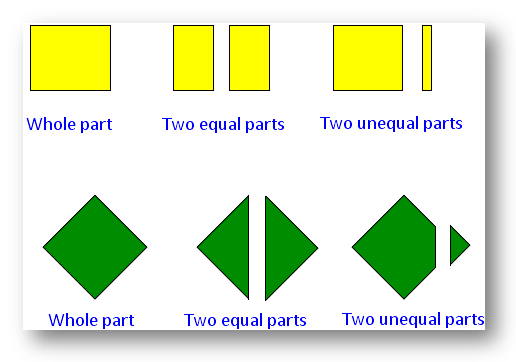
When an object as a whole is divided into two parts, there are two possibilities. The parts may be equal or unequal.
Each equal part of a whole is called one-half. It is expressed as \(\frac{1}{2}\) and read as one over two or one upon two.
In other words,
When we divide something into two equal parts each part is called one half of the whole. We also write it as \(\frac{1}{2}\).
(i)
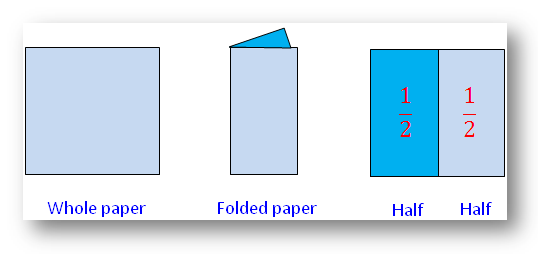
If a colorful sheet of paper is taken and one edge is brought on to the opposite edge and a crease is made in the middle, then this crease divides the sheet of paper into two equal parts. Each part will be one half of the whole sheet.
(ii)
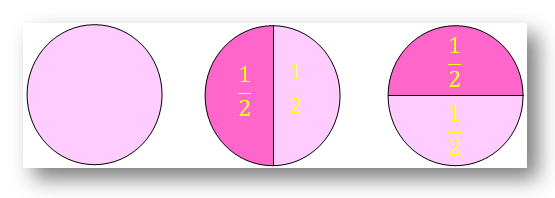
The circle is also be divided into two half circles. Each of the two equal parts is called half of the whole. Similarly, each of the two equal parts of a square is known as the half fraction as a part of a whole.
(iii)
This cake is divided into 2 equal parts. Each part is one half of the whole.
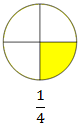
2. Fourths -
Again if we take a sheet which was earlier divided into two equal parts by folding, it can again be divided by a second fold in the middle.
In other words,
When we divide something into four equal parts each part is called one fourth of the whole. We also write it as \(\frac{1}{4}\).
(i)
Thus, the sheet is divided into four equal parts. Each equal part is called one-fourth or a quarter of the whole sheet. Thus, any whole can be divided into four equal parts and each part is one-fourth or a quarter of the whole. It is expressed as 1/4 and read as one over four or one upon four.
If we consider two parts of the four equal parts of a whole it will represent 2/4 or two fourths, i.e. two one-fourth or half.
If we consider three parts of the four equal parts of a whole, it will represent 3/4 or three-fourths or three quarters. It is also read as three upon four.
(ii)
This biscuit is divided into 4 equal parts. Each part is one fourth of the whole.
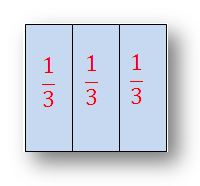
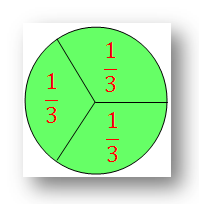
3. Thirds -
If a sheet is divided into three equal parts, then each part is called one-third of the whole sheet.
In other words,
When we divide something into three equal parts each part is called one third of the whole. We also write it as \(\frac{1}{3}\).
(i)
|
Thus, one of the three equal parts of a whole is called one-third of it and expressed as 1/3, which is written as one-third or one upon three. See the pictures shows three equal parts of a sheet. → |
(ii)
|
Similarly, if a circle is divided into three equal parts, each part is called one-third of the whole circle. One third is represented by 1/3 or, one upon three or, one three. See the pictures shows three equal parts of a circle. → |
(iii)
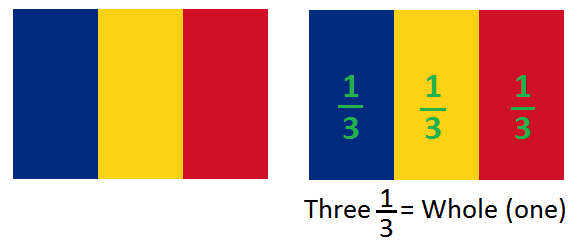
This Romanian flag is divided into 3 equal parts. Each part is one third of the whole.
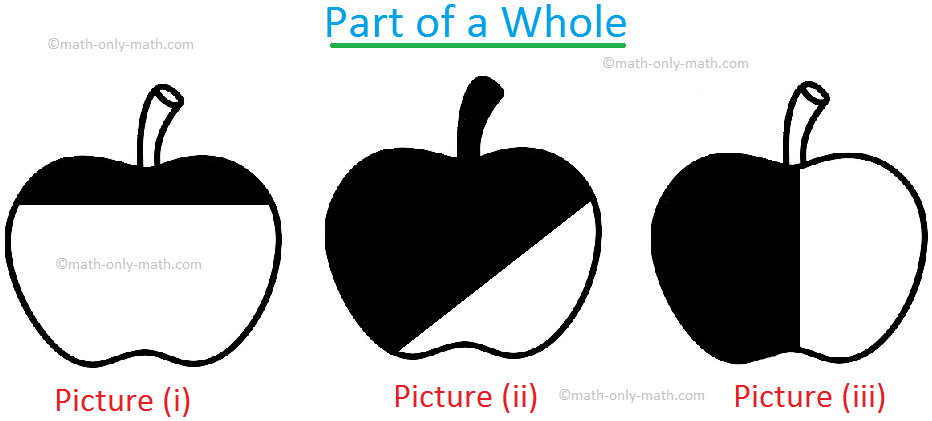
4. How can we fairly share one apple between two children? How much will each child get? Let us cut the apple in three different ways.
Now, let us compare the shaded parts which the unsheded parts in each picture. In picture (i) the shaded part is smaller than the unshaded part. In picture (ii) the shaded part is larger than the unshaded part. In p[icture (iii) shaded and unshaded parts are equal. We say that apple is divided into equal halves. One part is called one-half.
There are two halves in a whole. Each half is written as \(\frac{1}{2}\). It is read as one by two.
5. 1/2, 1/3, 2/4, 2/3, 3/4, ……… , etc., are called fractions or fractional numbers.
1/5, 2/5, 3/5, 4/5, 5/5, 1/6, 2/6, 3/6, 4/6, 5/6, ………… etc., are also fractions. Any part or part of a whole one is known as a fraction. A fraction is expressed by two numbers having a small horizontal line between them.
The number above the small line is called the numerator or top number and the number below the small line is called denominator or bottom number.
As, in 4/5, where 4 is the numerator and 5 is the denominator
\[\frac{4 {\color{Red} \rightarrow } Numerator}{5 {\color{Red} \rightarrow } Denominator}\]
We say one whole is divide into 5 equal parts from which if 4 parts are taken, it may be expressed as 4/5 which is a fractional number or fraction.
The above explanation will help us to understand how the fraction as a part of a whole number.
Related Concepts
● Fraction as a Part of Collection
● Convert a Fraction to an Equivalent Fraction
● Proper Fraction and Improper Fraction
From Fraction as a Part of a Whole to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
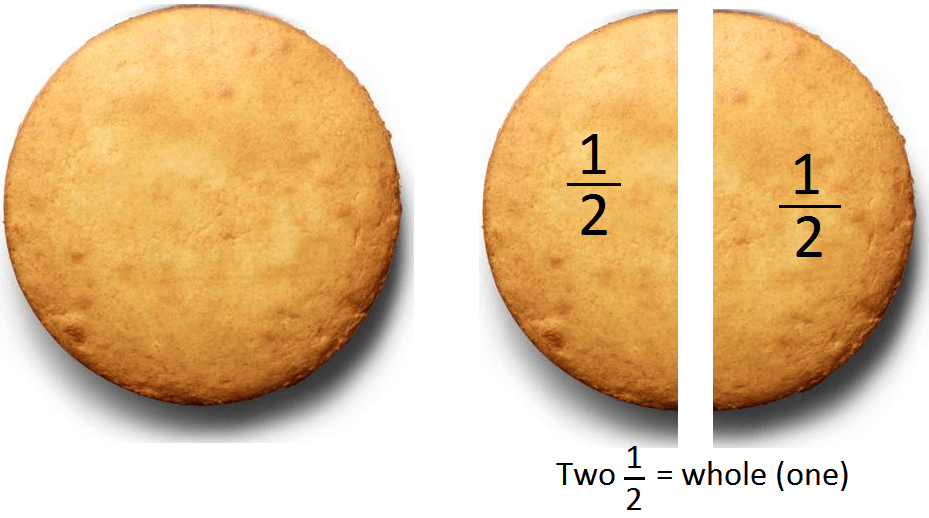
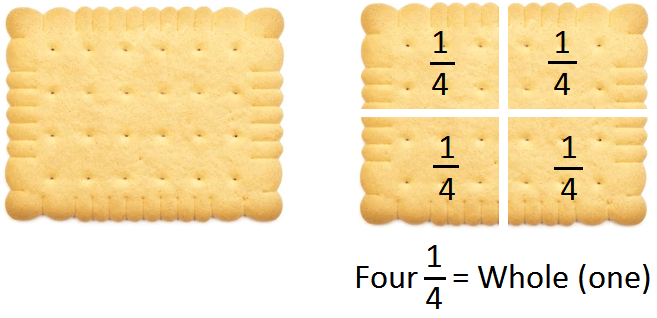


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.