Circumcircle of a Triangle

We will discuss here the Circumcircle of a Triangle and the circumcentre of a triangle.

A tangent that passes through the three vertices of a triangle is known as the circumcircle of the triangle.

When the vertices of a triangle lie on a circle, the sides of the triangle form chords of the circle.

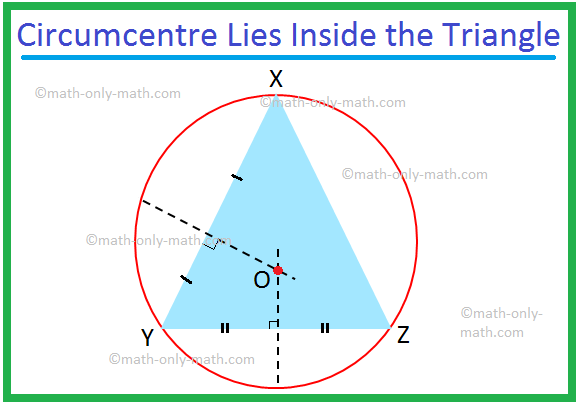
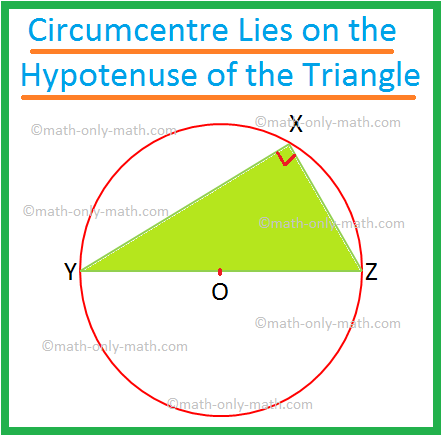
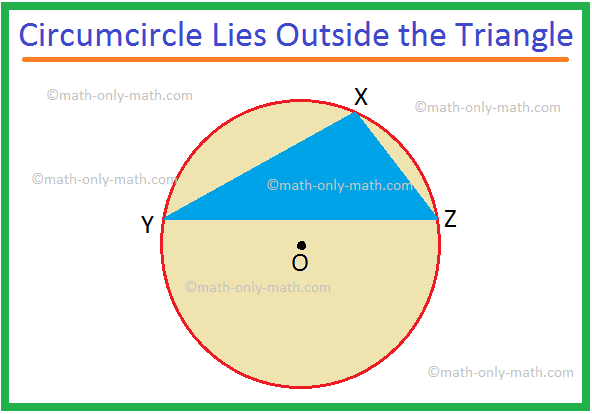
Hence, the centre of the circle is located at the point of intersection of the perpendicular bisectors of the sides of the triangle. This point is known as the circumcentre of the triangle. The radius of the circumcircle is equal to the distance between the circumcentre and any one of the three vertices of the triangle. The circumcentre of a triangle is equidistance from the three vertices. In each of the given figures, the circumcircle of ∆XYZ is the circle with centre O and radius equal to OX, or OY, or OZ.

If ∆XYZ is an acute-angled triangle, as in (i), the circumcentre lies inside the triangle.

If ∆XYZ is a right-angled triangle, as in (ii), the circumcentre lies on the hypotenuse of the triangle (since, the angle in a semicircle is a right angle).

If ∆XYZ is an obtuse-angled triangle, as in (ii), the circumcircle lies outside the triangle.

10th Grade Math

From Circumcircle of a Triangle to HOME PAGE