Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Three Digit Numbers
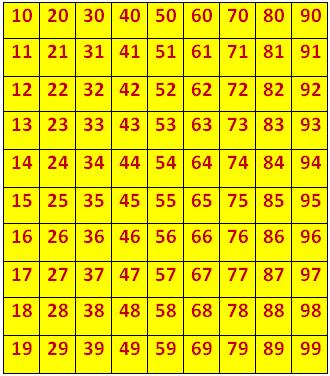
Three digit numbers are from 100 to 999. We know that there are nine one-digit numbers, i.e., 1, 2, 3, 4, 5, 6, 7, 8 and 9. There are 90 two digit numbers i.e., from 10 to 99. One digit numbers are made by the digits 1, 2, 3, 4, 5, 6, 7, 8 and 9. In making two digit numbers, zero (0) is also utilized along with digits 1 to 9. In two digit numbers one digit represents number of ones and the other represent the number of tens.
The digit representing ones is placed at one’s place while the digit representing ten’s is placed at ten’s place. As in 52, 5 is at ten’s place having its value 5 × 10 = 50 and 2 is at one’s place having it’s value 2 × 1 = 2.
Similarly, in 35, 5 is at one’s place having it’s value 5 × 1 = 5 and 3 is at ten’s place having its value 3 × 10 = 30 i.e., 35 = 30 + 5.
In the first ten two digits numbers the digits 0, 1, 2, …. are placed after 1 i.e., 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19. Then comes 2 at ten’s place. All the digits are placed after 2 i.e., 21, 22, 23, 24, 25, 26, 27, 28 and 29.
The following table shows the formation of two digits numbers:
Sophia has 99 beads. She uses 10 beads to make 1 garland. She has made 9 garlands and now she is left with 9 beads.
99 = 9 tens and 9 ones
She gets 1 more beads from her mother. She is now able to make another garland of 10 beads.
The total number of beads now 100.
99 and 1 more make 100
Ninety-nine and one more make one hundred.
THREE-DIGIT NUMBERS
In class 1, we have read about 1-digit and 2-digit numbers. We know how to read and write these numbers. We also know that:
The smallest 1-digit number is 1.
The largest 1-digit number is 9.
The smallest 2-digit number is 10.
The largest 2-digit number is 99.
Let us add 1 to 99.
99 + 1 = 90 + 9 + 1
= 9 tens + 9 ones + 1 one
= 9 tens + 10 ones
= 9 tens + 1 ten [since, 10 ones = 1 ten]
= 10 tens
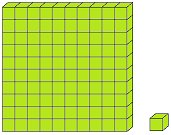
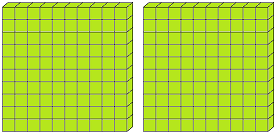
We call 10 tens as one hundred and write it as 100.
100 is smallest 3-digit number.
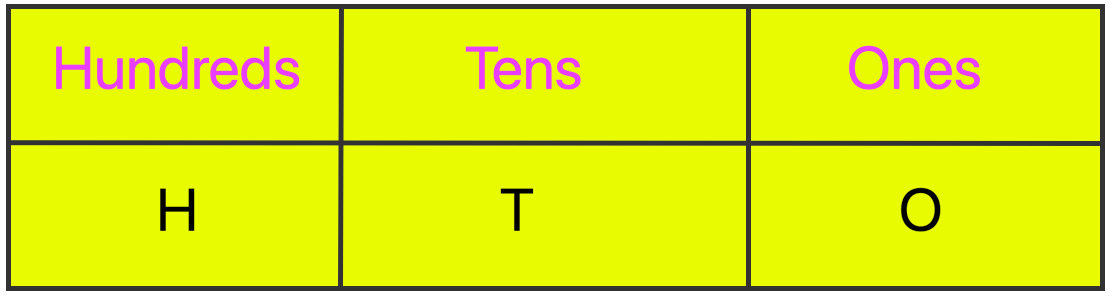
In a 3-digit number:
The first place from the right is one's place.
The second place from the right is ten's place.
The third place from the right is hundred's place.
Thus, we have the chart as shown below:
What comes after 99?
The number is 100. It is written in words as one hundred. It is a 3-digit number.
We can say that ninety-nine and one more = One hundred.
Using tens, we say that 10 tens = 1 hundred.
So, after 99, the counting number is 100. This is a three digit number. When one is added to 99, the sum is 100.
The smallest 3-digit number and 1 more is 100 + 1 = 101
101 and 1 more is 101 + 1 = 102
102 and 1 more is 102 + 1 = 103
In this way, we write up to 999 which is largest 3-digit number.
In 100, there are 10 tens or 100 ones, i.e., (100 = 10 × 10 = 100 × 1). With the help of ones we get tens and with the help of ones and tens we make the numbers of two digits, i.e., from 10 to 99.
We know that
One ten = ten (10)
Two tens = twenty (20)
Three tens = thirty (30)
Four tens = forty (40)
Five tens = fifty (50)
Six tens = sixty (60)
Seven tens = seventy (70)
Eight tens = eighty (80)
Nine tens = ninety (90)
Ten tens = one hundred (100)
Similarly,
1 × hundred = hundred (100)
2 × hundred = two hundred (200)
3 × hundred = three hundred (300)
4 × hundred = four hundred (400)
5 × hundred = five hundred (500)
6 × hundred = six hundred (600)
7 × hundred = seven hundred (700)
8 × hundred = eight hundred (800)
9 × hundred = nine hundred (900)
10 × hundred = ten hundred (1000)
We see that the three digit numbers like 100, 200, 300, 400, 500, 600, 700, 800 and 900 are represented by the numerals having a digit and two zeros. This numbers are the multiples of two numbers i.e., 100 × 1, 110 × 2, 100 × 3, …….., etc.
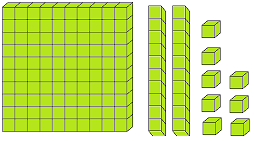
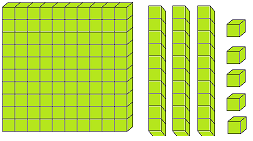
But the three digit numbers are formed by placing the one and two digit numbers, i.e., from 1 to 99 after the fundamental digits 1, 2, 3, ….., 9 respectively as 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, ……., 117, 118, 119, ………, 125, 126, 127, …….., 134, 135, 136, ……….., 299, 300, 301, ….…., 400, ….…, 427, ………….etc.
In three digit numbers the digits are placed at one’s, ten’s and hundred’s place. At the extreme right of the number there is one’s place, then to the left of it there is ten’s place and to the left of it there is hundred’s place. The digits have their place value in a given number.
For example, in 235 the place value of 5 is 5, of 3 is 30 and 2 is 200. We write this in words as two hundred thirty five.
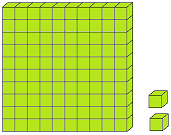
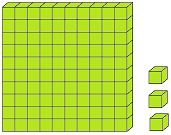
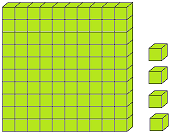
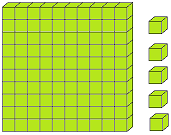
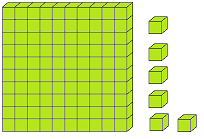
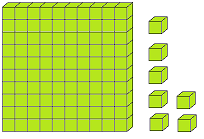
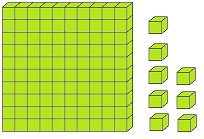
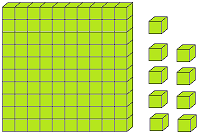
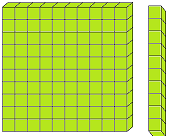
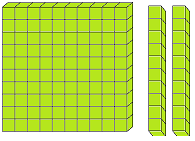
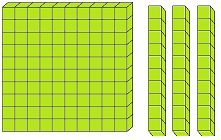
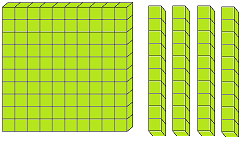
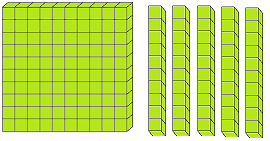
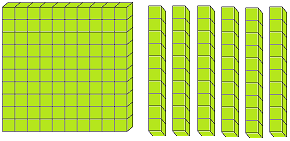
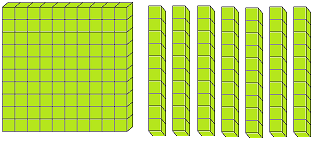
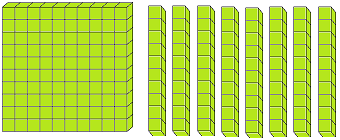
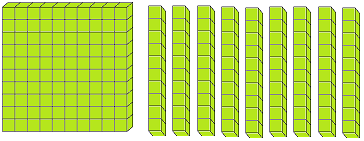
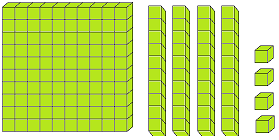
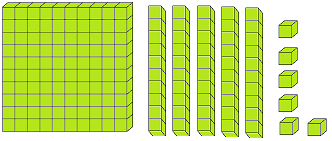
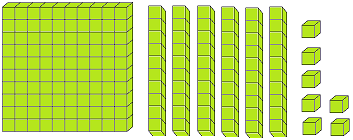
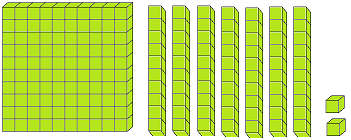
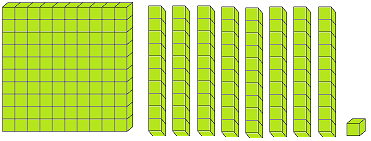
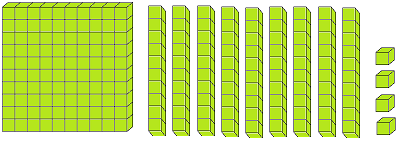
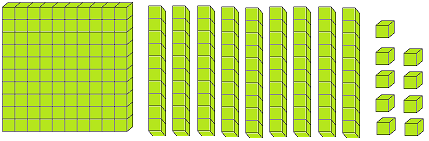
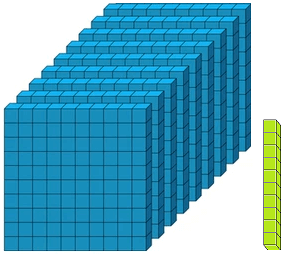
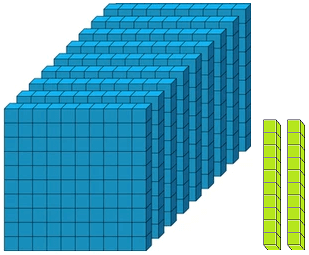
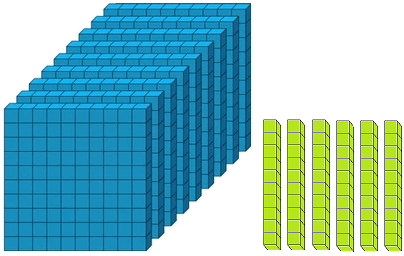
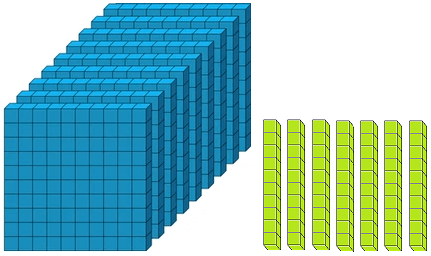
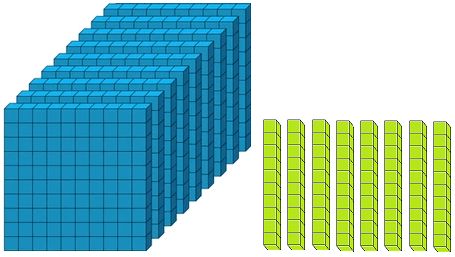
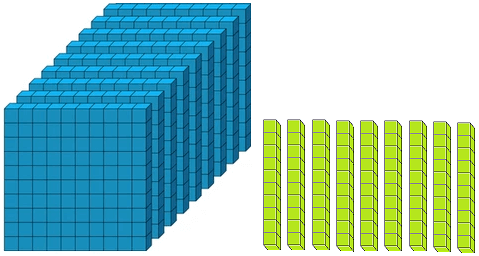
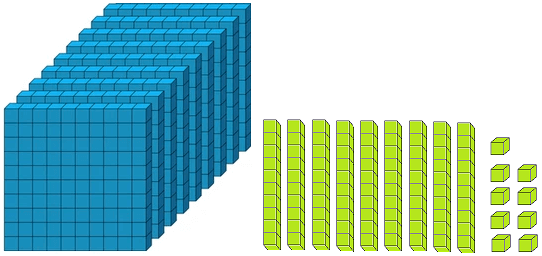
Let us form the number 100 with the help of blocks. If we say one small block is 1 then a strip made of 10 small blocks will represent 10. A sheet made of 10 strips will show 100.
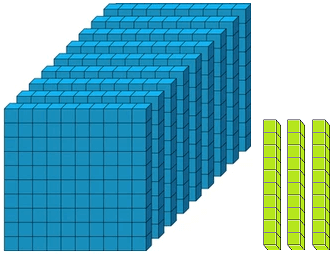
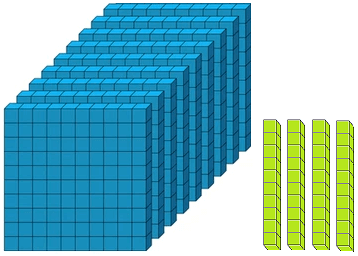
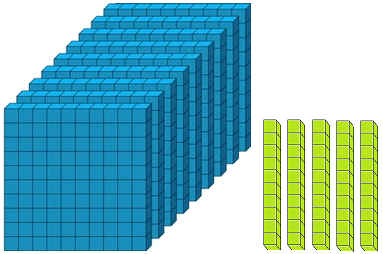
Numbers from 101 to 110
Numbers from 110 to 200
|
110 |
One hundred ten | |
|
120 |
One hundred twenty | |
|
130 |
One hundred thirty | |
|
140 |
One hundred forty | |
|
150 |
One hundred fifty | |
|
160 |
One hundred sixty | |
|
170 |
One hundred seventy | |
|
180 |
One hundred eighty | |
|
190 |
One hundred ninety | |
|
200 |
Two hundred |
Count and write the number and number name.
|
117 |
One hundred seventeen | |
|
128 |
One hundred twenty-eight | |
|
135 |
One hundred thirty-five | |
|
144 |
One hundred forty-four | |
|
156 |
One hundred fifty-six | |
|
167 |
One hundred sixty-seven | |
|
172 |
One hundred seventy-two | |
|
181 |
One hundred eighty-one | |
|
194 |
One hundred ninety-four | |
|
199 |
One hundred ninety-nine |
Skip Counting in Hundreds
It is easier to count larger numbers by making groups of hundreds.
 |
100 |
One hundred |
|
200 |
Two hundred | |
|
300 |
Three hundred | |
|
400 |
Four hundred | |
|
500 |
Five hundred | |
|
600 |
Six hundred | |
|
700 |
Seven hundred | |
|
800 |
Eight hundred | |
|
900 |
Nine hundred |
Count and write the number and number names.
|
910 |
Nine hundred ten | |
|
920 |
Nine hundred twenty | |
|
930 |
Nine hundred thirty | |
|
940 |
Nine hundred forty | |
|
950 |
Nine hundred fifty | |
|
960 |
Nine hundred sixty | |
|
970 |
Nine hundred seventy | |
|
980 |
Nine hundred eighty | |
|
990 |
Nine hundred ninety | |
|
999 |
Nine hundred ninety-nine |
Some numbers between 101 and 999 are given below:
|
Number Name One hundred one One hundred two One hundred three One hundred four One hundred five One hundred ten One hundred eleven One hundred nineteen One hundred twenty One hundred twenty-one One hundred thirty One hundred thirty-one One hundred forty One hundred forty-one One hundred fifty One hundred fifty-one One hundred sixty One hundred sixty-one One hundred seventy One hundred seventy-one One hundred eighty One hundred eighty-one One hundred ninety One hundred ninety-one One hundred ninety-nine Two hundred Two hundred one Two hundred two Two hundred ninety-nine Three hundred Three hundred one Three hundred ninety-nine Four hundred Four hundred-one Four hundred fifty Four hundred fifty-one Four hundred ninety-nine Five hundred Five hundred one Five hundred ninety-nine Six hundred Six hundred ninety-nine Seven hundred Seven hundred one Seven hundred ninety-nine Eight hundred Eight hundred ninety-nine Nine hundred Nine hundred ninety-nine |
Numeral 101 102 103 104 105 and so on 110 111 and so on 119 120 121 and so on 130 131 and so on 140 141 and so on 150 151 and so on 160 161 and so on 170 171 and so on 180 181 and so on 190 191 and so on 199 200 201 202 and so on 299 300 301 and so on 399 400 401 and so on 450 451 and so on 499 500 501 and so on 599 600 and so on 699 700 701 and so on 799
900 and so on 999 |
To read a 3-digit number, we first read the hundred's place followed by the number formed by the last two digits.
Note: The number name denotes how we read a numeral.
Remember: 3-digit numbers start with 100 and end at 999. There are 900, 3-digit numbers in all.
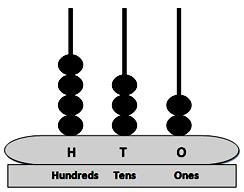
The three digits numbers may easily be explained with the help of mathematical apparatus called ABACUS.
What is spike abacus?
Spike abacus has many iron spikes on a wooden base. The spikes may have globules having wholes. The spikes are named as ones, tens, hundreds, thousands etc. respectively from extreme right to the left.
The number of globules in the concerned spikes expresses the place value of the digit of the number.
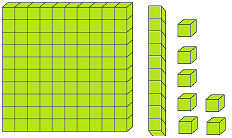
In the given picture of the abacus, there are three spikes. In the first spike expressing ones, there are 2 globules, next to it there are 3 globules and in the third spike from the ones’ spike there are 4 globules.
2 globules of the one’s mark, spike express 2 × 1 = 2, 3 globules of the tens spike express 3 × 10 = 30 while 4 globule of the third spike i.e., hundreds spike express 4 × 100 = 400. Thus, the globules placed at different places represent the number 400 + 30 + 2 = 432.
Thus, with the help of ‘abacus’ we can understand the concept of three digit numbers.
Review:
● A number has one or more than one digit.
● To write the numbers we use digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
● A number which has single digit like 1, 2, 3, ............. 9 are called one digit numbers.
● A number which has double digits like 22, 53, 67, ............... 99 are called two digits number.
● A number which has triple digits like 100, 235, 367, ............... 999 are called three digits number.
● To read a two-digits number, first read the tens place and then read the ones place.
● To read a three digits number, first read the hundreds place, then read the last two digits as shown below.
Expanded and Short Form of 3-Digit Numbers:
Look at the given example:
Solved Examples on Expanded and Short Form of 3-Digit Numbers:
1. Write in Expanded Form:
(i) 792 = _____ + _____ + _____
(ii) 247 = _____ + _____ + _____
(iii) 618 = _____ + _____ + _____
(iv) 864 = _____ + _____ + _____
Solution:
1. (i) 792 = 700 + 90 + 2
(ii) 247 = 200 + 40 + 7
(iii) 618 = 600 + 10 + 8
(iv) 864 = 800 + 60 + 4
2. Write in short form:
(i) 300 + 80 + 9
(ii) 900 + 10 + 9
(iii) 100 + 20 + 0
(iv) 600 + 50 + 4
Solution:
2. (i)389
(ii) 919
(iii) 120
(iv) 654
Worksheet on 3-Digit Numbers:
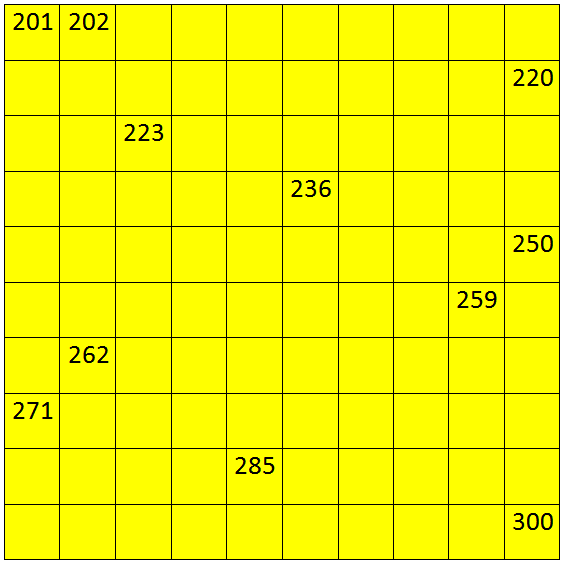
I. Write the numbers from 101 to 200.
II. Write the numbers from 201 to 300.
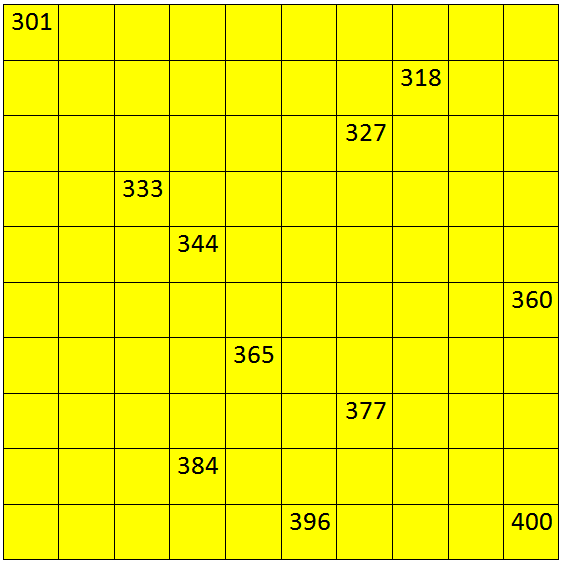
III. Write the numbers from 301 to 400.
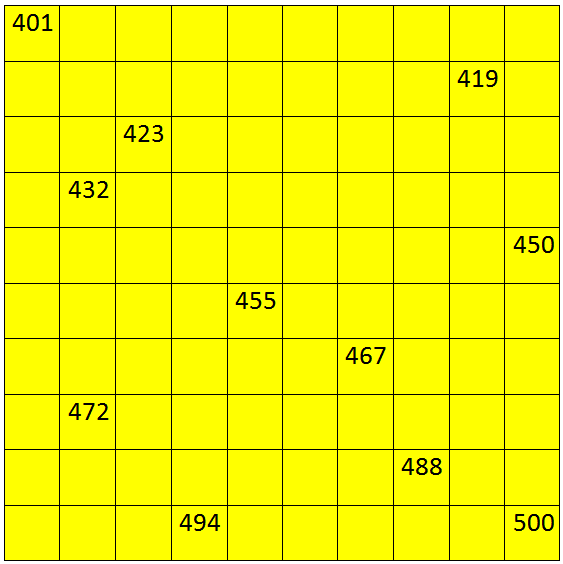
IV. Write the numbers from 401 to 500.
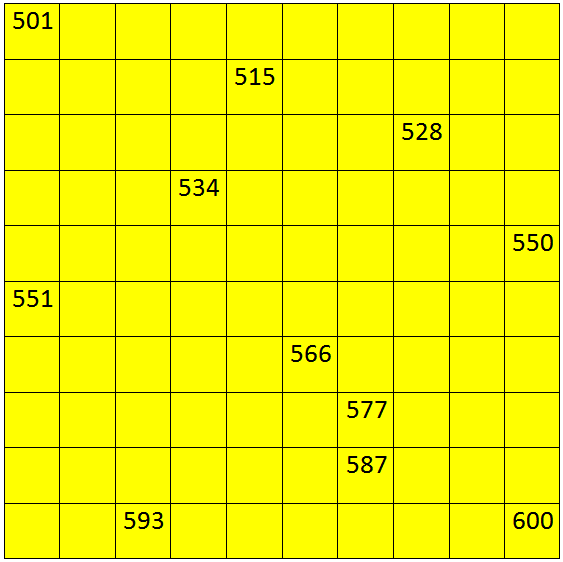
V. Write the numbers from 501 to 600.
VI. Write 321 to 350:
|
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
|
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
|
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
VII. Write 581 to 610:
|
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
|
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
|
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
VIII. Fill in the blanks:
|
378 |
379 |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
|
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
397 |
|
___ |
___ |
400 |
___ |
___ |
___ |
___ |
___ |
___ |
___ |
IX. Write the short forms. One has been done for you.
|
H |
T |
O | |||
|
600 |
+ |
20 |
+ |
3 |
= 623 |
|
300 |
+ |
0 |
+ |
8 |
= _____ |
|
400 |
+ |
30 |
+ |
0 |
= _____ |
|
800 |
+ |
50 |
+ |
9 |
= _____ |
|
700 |
+ |
80 |
+ |
7 |
= _____ |
|
70 |
+ |
9 |
= _____ | ||
|
500 |
+ |
90 |
+ |
5 |
= _____ |
X. Write in the expanded forms. One has been done for you.
|
H |
T |
O | |||
|
420 = |
400 |
+ |
20 |
+ |
0 |
|
576 = |
____ |
+ |
____ |
+ |
____ |
|
684 = |
____ |
+ |
____ |
+ |
____ |
|
769 = |
____ |
+ |
____ |
+ |
____ |
|
845 = |
____ |
+ |
____ |
+ |
____ |
|
367 = |
____ |
+ |
____ |
+ |
____ |
|
296 = |
____ |
+ |
____ |
+ |
____ |
XI. Fill in the blanks:
(i) 648 = ............ hundreds + ............ tens + ............ ones
(ii) 735 = ............ hundreds + ............ tens + ............ ones
(iii) 290 = ............ hundreds + ............ tens + ............ ones
(iv) 579 = ............ hundreds + ............ tens + ............ ones
XII. Write the number names:
(i) 326 -
(ii) 578 -
(iii) 729 -
(iv) 107 -
(v) 450 -
(vi) 672 -
(vii) 762 -
(viii) 985
(ix) 855 -
(x) 736 -
(xi) 244 -
(xii) 790 -
(xiii) 189 -
XIII. Write the numbers:
(i) Six hundred ninety two
(ii) Two hundred thirty eight
(iii) Seven hundred twenty one
(iv) one hundred forty
(v) Five hundred twelve
(vi) Four hundred six
(vii) Eight hundred thirty two
(viii) Five hundred eighty nine
(ix) Nine hundred forty seven
(x) Nine hundred ninety nine
(xi) Three hundred ninety eight
(xii) Two hundred fifty three
XIV. Write the expanded form. One has been done for you.
(i) 358 = Three hundreds and five tens and eight ones
(ii) 156 = ___________________________________
(iii) 653 = ___________________________________
(iv) 241 = ___________________________________
(v) 586 = ___________________________________
XV. Write in words. One has been done for you.
(i) 135 = One hundred and thirty-five
(ii) 980 = ___________________________________
(iii) 760 = ___________________________________
(iv) 332 = ___________________________________
(v) 973 = ___________________________________
XVI. Write the numbers in the blanks. One has been done for you.
|
(i) Nine hundred and ninety-nine. (ii) Nine hundred. (iii) One hundred and seventy-three. (iv) Eight hundred. |
999 _____ _____ _____ |
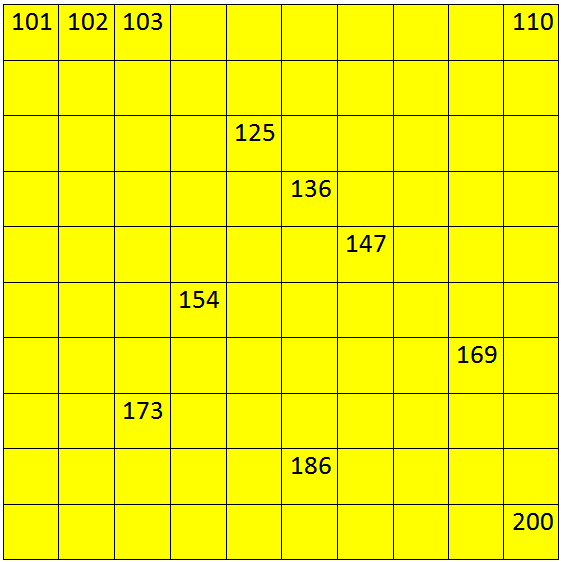
XVII: Fill in the missing numbers.
XVIII. Fill in the boxes with numbers before, after or between.
|
Before |
Between |
After | |
|
(i) |
.............. |
280 |
.............. |
|
(ii) |
193 |
.............. |
.............. |
|
(iii) |
.............. |
.............. |
181 |
|
(iv) |
.............. |
700 |
.............. |
|
(v) |
.............. |
349 |
.............. |
|
(vi) |
899 |
.............. |
901 |
From Three Digit Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.









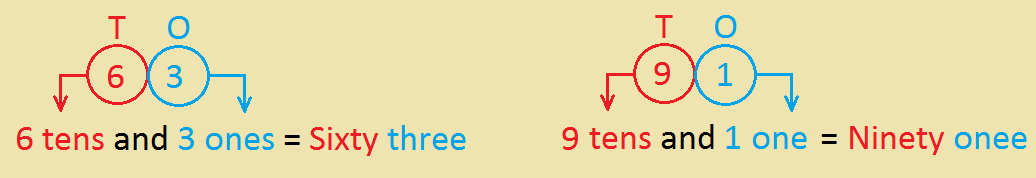




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.