Subscribe to our YouTube channel for the latest videos, updates, and tips.
Solving Algebraic Fractions
Solving algebraic fractions to its lowest term follow the step-by-step explanation given below.
1. Simplify the algebraic fractions: x−28−2(2x+3)3+11x−36
Solution:
x−28−2(2x+3)3+11x−36
= 3(x−2)−16(2x+3)+4(11x−3)24
= 3x−6−32x−48+44x−1224
= 15x−6624
= 3(5x−22)24
= 5x−228
2. Reduce the algebraic fractions: 2aa−2−a2a2−4
Solution:
2aa−2−a2a2−4
= 2aa−2−a2a2−22
= 2aa−2−a2(a+2)(a−2)
= 2a(a+2)−a2(a+2)(a−2)
= 2a2+4a−a2a2−4
= a2+4aa2−4
3. Reduce to lowest terms -- if possible: 2a+b−3a−b+6aa2−b2
Solution:
2a+b−3a−b+6aa2−b2
= 2(a−b)−3(a+b)+6a(a+b)(a−b)
= 2a−2b−3a−3b+6aa2−b2
= 5a−5ba2−b2
= 5(a−b)(a+b)(a−b)
= 5(a+b)
4. simplify and Reduce: 3xx2−9+1x2+2x−15
Solution:
3xx2−9+1x2+2x−15
Step 1: Factorize the polynomials separately first:
(i) x2 – 9 = (x + 3) (x – 3)
(ii) x2 + 2x – 15 = x2 + 5x – 3x – 15
= x(x + 5) – 3(x + 5)
= (x + 5) (x – 3)
Step 2: Simplify by substituting with the factors:
3xx2−9+1x2+2x−15
= 3x(x+3)(x−3)+1(x+5)(x−3)
= 3x(x+5)+x+3(x+3)(x−3)(x+5)
= 3x2+15x+x+3(x+3)(x−3)(x+5)
= 3x2+16x+3(x+3)(x−3)(x+5)
8th Grade Math Practice
From Solving Algebraic Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
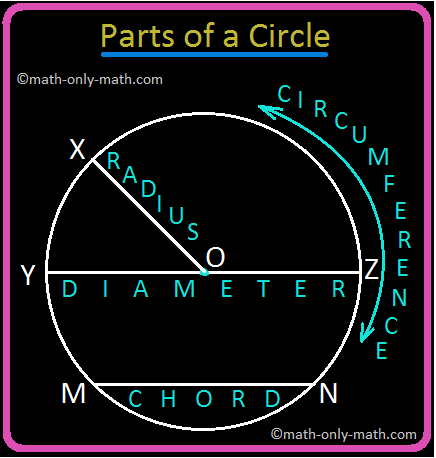
5th Grade Circle Worksheet | Free Worksheet with Answer |Practice Math
Jul 10, 25 11:41 AM
In 5th Grade Circle Worksheet you will get different types of questions on parts of a circle, relation between radius and diameter, interior of a circle, exterior of a circle and construction of circl… -
Construction of a Circle | Working Rules | Step-by-step Explanation |
Jul 09, 25 01:29 AM
Construction of a Circle when the length of its Radius is given. Working Rules | Step I: Open the compass such that its pointer be put on initial point (i.e. O) of ruler / scale and the pencil-end be… -
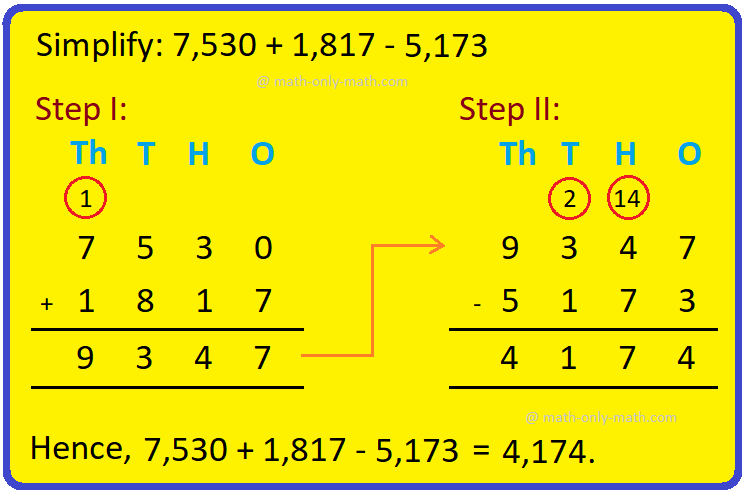
Combination of Addition and Subtraction | Mixed Addition & Subtraction
Jul 08, 25 02:32 PM
We will discuss here about the combination of addition and subtraction. The rules which can be used to solve the sums involving addition (+) and subtraction (-) together are: I: First add -
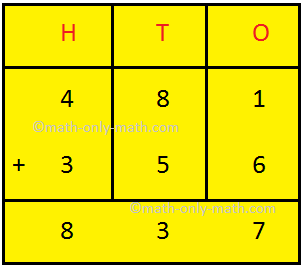
Addition & Subtraction Together |Combination of addition & subtraction
Jul 08, 25 02:23 PM
We will solve the different types of problems involving addition and subtraction together. To show the problem involving both addition and subtraction, we first group all the numbers with ‘+’ and… -
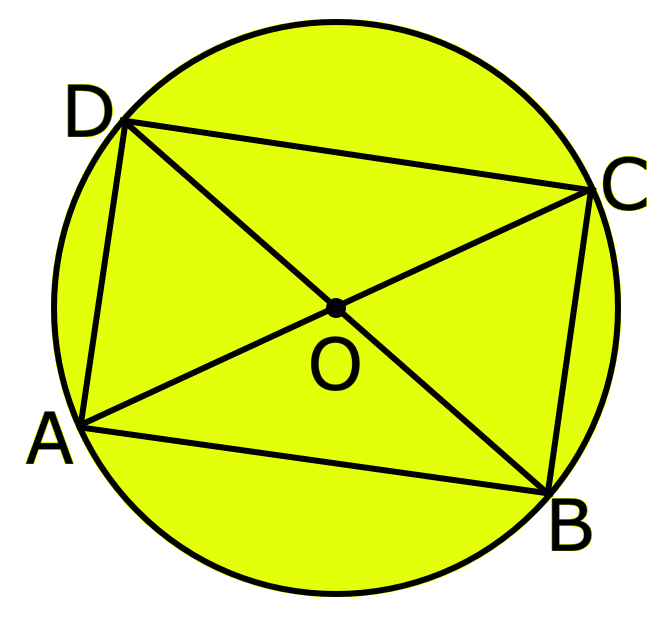
5th Grade Circle | Radius, Interior and Exterior of a Circle|Worksheet
Jul 08, 25 09:55 AM
A circle is the set of all those point in a plane whose distance from a fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.