Properties of a Rectangle Rhombus and Square

The properties of a rectangle, rhombus and square are discussed here using figure.

Diagonal Properties of a Rectangle

Prove that the diagonals of a rectangle are equal and bisect each other.

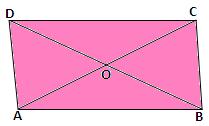
Let ABCD be a rectangle whose diagonals AC and BD intersect at the point 0. 

From ∆ ABC and ∆ BAD, 

AB = BA (common) 

∠ABC = ∠BAD (each equal to 90o) 

BC = AD (opposite sides of a rectangle). 

Therefore, ∆ ABC ≅ ∆ BAD (by SAS congruence) 

⇒ AC = BD. 

Hence, the diagonals of a rectangle are equal. 

From ∆ OAB and ∆ OCD,

∠OAB = ∠OCD (alternate angles)

∠OBA = ∠ODC (alternate angles)

AB = CD (opposite sides of a rectangle)

Therefore, ∆OAB ≅ ∆ OCD. (by ASA congruence)

⇒ OA = OC and OB = OD.

This shows that the diagonals of a rectangle bisect each other.

Hence, the diagonals of a rectangle are equal and bisect each other.

Diagonal Properties of a Rhombus

Prove that the diagonals of a rhombus bisect each other at right angles.

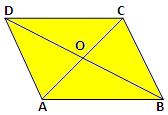
Let ABCD be a rhombus whose diagonals AC and BD intersect at the point O.

We know that the diagonals of a parallelogram bisect each other.

Also, we know that every rhombus is a parallelogram.

So, the diagonals of a rhombus bisect each other.

Therefore, OA = OC and OB = OD

From ∆ COB and ∆ COD,

CB = CD (sides of a rhombus)

CO = CO (common).

OB = OD (proved)

Therefore, ∆ COB ≅ ∆ COD (by SSS congruence)

⇒ ∠COB = ∠COD

But, ∠COB + ∠COD = 2 right angles (linear pair)

Therefore, ∠COB = ∠COD = 1 right angle.

Hence, the diagonals of a rhombus bisect each other at right angles.


`

Diagonal Properties of a Square

Prove that the diagonals of a square are equal and bisect each other at right angles.

We know that the diagonals of a rectangle are equal.

Also, we know that every square is a rectangle.

So, the diagonals of a square are equal.

Again, we know that the diagonals of a rhombus bisect each other at right angles. But, every square is a rhombus.

So, the diagonals of a square bisect each other at right angles.

Hence, the diagonals of a square are equal and bisect each other at right angles.

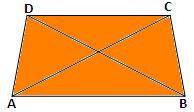
NOTE 1:

If the diagonals of a quadrilateral are equal then it is not necessarily a rectangle.

In the adjacent figure, ABCD is a quadrilateral in which diagonal AC = diagonal BD, but ABCD is not a rectangle.

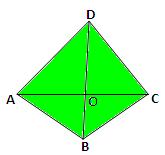
NOTE 2:

If the diagonals of a quadrilateral intersect at right angles then it is not necessarily a rhombus.

Parallelogram

Parallelogram

Properties of a Rectangle Rhombus and Square

Problems on Parallelogram

Practice Test on Parallelogram

Parallelogram - Worksheet

Worksheet on Parallelogram

8th Grade Math Practice

From Properties of a Rectangle Rhombus and Square to HOME PAGE